 |
Just like Transformations in Geometry, podemos mover e redimensionar os gráficos de funções |
Deixe-nos começar com uma função, neste caso é f(x) = x2, mas pode ser qualquer coisa:
f(x) = x2
Aqui estão algumas coisas simples que podemos fazer para a mover ou escalar no gráfico:
Podemos movê-la para cima ou para baixo adicionando uma constante ao valor y:
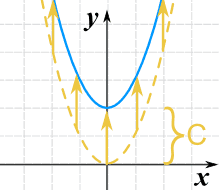
g(x) = x2 + C
Nota: para mover a linha para baixo, usamos um valor negativo para C.
- C > 0 move-o para cima
- C < 0 move-o para baixo
Podemos movê-lo para a esquerda ou para a direita, adicionando uma constante ao valor x:
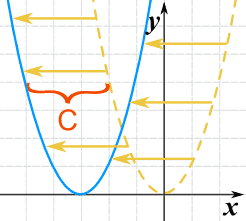
g(x) = (x+C)2
Adding C move a função para a esquerda (a direcção negativa).
Porquê? Bem, imagine que herdará uma fortuna quando a sua idade=25 anos. Se mudar isso para (idade+4) = 25 anos, então receberá quando tiver 21 anos. Adicionando 4 fez acontecer antes.
- C > 0 move-o para a esquerda
- C < 0 move-o para a direita
MAS temos de adicionar C onde x aparecer na função (estamos a substituir x+C por x).
Exemplo: a função v(x) = x3 – x2 + 4x
Para mover espaços C para a esquerda, adicionar C a x onde x aparecer:
w(x) = (x + C)3 – (x + C)2 + 4(x + C)
Uma forma fácil de lembrar o que acontece ao gráfico quando adicionamos uma constante:
add to y para ir alto
add to x para ir para a esquerda
Podemos esticá-lo ou comprimi-lo no sentido y multiplicando toda a função por uma constante.
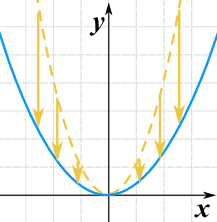
g(x) = 0.35(x2)
- C > 1 estica-o
- 0 < C < 1 comprime-o
Podemos esticá-lo ou comprimi-lo no x-multiplicando x por uma constante.
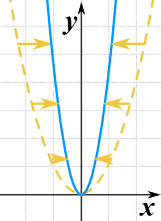
g(x) = (2x)2
- C > 1 compressas it
- 0 < C < 1 estica-o
Nota que (ao contrário do y-direcção), valores maiores causam mais compressão.
Podemos virá-lo ao contrário multiplicando toda a função por -1:
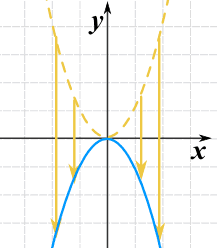
g(x) = -(x2)
Isto também é chamado reflexão sobre o eixo x (o eixo onde y=0)
Podemos combinar um valor negativo com uma escala:
Exemplo: a multiplicação por -2 virá-lo-á de cabeça para baixo E esticá-lo-á no sentido y.
Podemos virá-lo para a esquerda-direita multiplicando o valor x por -1:
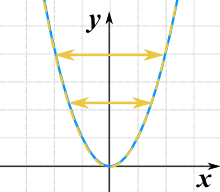
g(x) = (-x)2
Vira-o realmente para a esquerda e para a direita! Mas não se consegue vê-lo, porque x2 é simétrico em relação ao eixo y. Por isso, aqui está outro exemplo usando √(x):
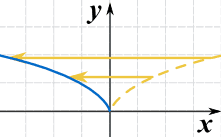
g(x) = √(-x)
p> Isto também é chamado reflexão sobre o y-eixo (o eixo onde x=0)
Sumário
| y = f(x) + C |
|
| y = f(x + C) |
|
| y = Cf(x) | ul>
|
| y = f(Cx) |
|
| y = -f(x) | ul>>>li>Reflecte-o sobre x-eixo |
Exemplos
Exemplo: a função g(x) = 1/x
Aqui estão algumas coisas que podemos fazer:
Exemplo: a função v(x) = x3 – 4x
Aqui estão algumas coisas que podemos fazer:
= 2×3 – 8x
= 27×3 – 12x
All In One …. !
Podemos fazer todas as transformações de uma só vez usando isto:
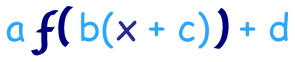
a é estiramento/compressão vertical
- |a| > 1 estiramentos
- |a| < 1 compressas
- a < 0 vira o gráfico do avesso down
b é estiramento/compressão horizontal
- |b| > 1 compresses
- |b| < 1 estiramentos
- b < 0 vira o gráfico para a esquerda-direita
c é turno horizontal
- c < 0 turnos para a direita
- c > 0 turnos para a esquerda
d é deslocamento vertical
- d < 0 turnos para baixo
- d > 0 turnos para cima
/li>
