Sabemos calcular a expressão 5 x 5. Esta expressão pode ser escrita de uma forma mais curta usando algo chamado expoentes.
$5\cdot 5=5^{2}$$
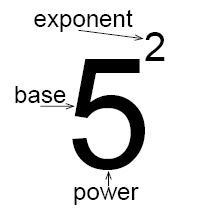
Uma expressão que representa a multiplicação repetida do mesmo factor é chamada de poder.
O número 5 é chamado de base, e o número 2 é chamado de expoente. O expoente corresponde ao número de vezes que a base é utilizada como um factor.
| 31 | 3 à primeira potência | 3 |
| 4 para a segunda potência ou 4 ao quadrado | 4 ∙ 4 | |
| 53 | 5 para a terceira potência ou 5 ao quadrado | 5 ∙ 5 ∙ 5 |
| 2 para a potência de six | 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 |
Exemplo
Escrever estas multiplicações como expoentes
$5\cdot 5\cdot 5=5^{3}$$
$4\cdot 4\cdot 4\cdot 4=4^{5}$$
$3\cdot 3\cdot 3=3^{4}$$
Multiplicação
Se duas potências têm a mesma base, então podemos multiplicar as potências. Quando multiplicamos duas potências, adicionamos os seus expoentes.
A regra:
$x^{a}}cdot x^{b}=x^{a+b}$$
p>Exemplo
$4^{2}cdot 4^{5}=esquerda ( 4=cdot 4 {direita ) {cdot {esquerda ( 4=cdot 4=cdot 4\cdot 4\cdot 4 {7}=4^{2+5}$$
Divisão
Se duas potências têm a mesma base, então podemos dividir as potências. Quando dividimos poderes, subtraímos os seus expoentes.
A regra:
$$frac{x^{a}}{ x^{b}}=x^{a-b}$$
Exemplo
p>$$frac{4^{2}{ 4^{5}=frac{{{\an8}=color{\an8}{4}não{4}cdot{\an8}cdot{\an8} 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não) 4 não)3}=4^{2-5}$$
Um expoente negativo é o mesmo que o recíproco do expoente positivo.
$x^{-a}==frac{1}{x^{a}}$$
Exemplo
$$2^{-3}=frac{1}{2^{3}}$$
Quando se eleva um produto a um poder, elevamos cada factor com um poder
$(x\cdot y)^{a}=x^{a}{a}{cdot y^{a}$
Exemplo
$(2x)^{4}=2^{4}{4}}cdot x^{4}=16x^{4}$$
A regra para o poder de um poder e o poder de um produto pode ser combinada na seguinte regra:
$(x^{a}}cdot y^{b})^{z}=x^{a^cdot z}cdot y^{b=cdot z}$$
Exemplo
$(x^{3}cdot y^{4})^{2}=x^{3}cdot 2}cdot y^{4}cdot 2}=x^{6}cdot y^{8}$$
Aulas de vídeo
Reescrever as expressões
$2\cdot 2\cdot 2$$
$x\cdot x\cdot x\cdot x\cdot x$