Transformaciones de funciones

Al igual que las Transformaciones en Geometría, podemos mover y redimensionar las gráficas de las funciones

Empecemos con una función, en este caso es f(x) = x2, pero podría ser cualquier cosa:

f(x) = x2

Aquí tenemos algunas cosas sencillas que podemos hacer para moverla o escalarla en la gráfica:

Podemos moverla hacia arriba o hacia abajo añadiendo una constante al valor de y:

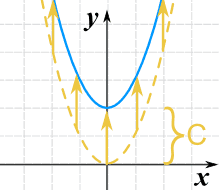
g(x) = x2 + C

Nota: para mover la recta hacia abajo, utilizamos un valor negativo para C.

• C > 0 lo mueve hacia arriba
• C < 0 lo mueve hacia abajo

Podemos moverlo a la izquierda o a la derecha añadiendo una constante al valor de x:

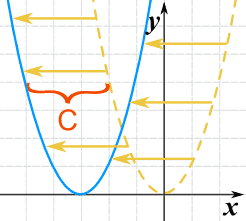
g(x) = (x+C)2

• C > 0 lo mueve a la izquierda
• C < 0 lo mueve a la derecha

Pero hay que añadir C donde aparezca x en la función (estamos sustituyendo x+C por x).

Ejemplo: la función v(x) = x3 – x2 + 4x

Para mover C espacios a la izquierda, hay que añadir C a x siempre que aparezca x:

w(x) = (x + C)3 – (x + C)2 + 4(x + C)

Una forma fácil de recordar lo que ocurre con la gráfica cuando añadimos una constante:

Añadir a y para ir hacia arriba
Añadir a x para ir hacia la izquierda

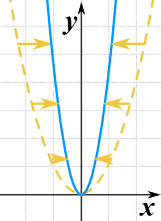
Podemos estirarla o comprimirla en la dirección y multiplicando toda la función por una constante.



g(x) = 0.35(x2)

• C > 1 lo estira
• 0 << 1 lo comprime

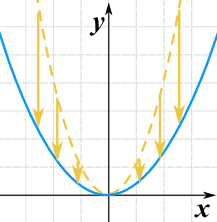
Podemos estirarlo o comprimirlo en la x-dirección multiplicando x por una constante.



g(x) = (2x)2

• C > 1 lo comprime lo
• 0 < C < 1 lo estira

Nótese que (a diferencia de lo que ocurre con la y-dirección), los valores más grandes provocan una mayor compresión.

Podemos darle la vuelta multiplicando toda la función por -1:



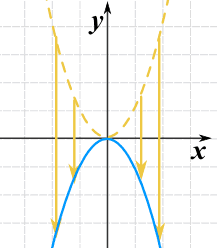
g(x) = -(x2)

También se llama reflexión sobre el eje x (el eje donde y=0)

Podemos combinar un valor negativo con un escalado:

Ejemplo: al multiplicar por -2 lo voltearemos y lo estiraremos en la dirección y.

Podemos voltearlo a la izquierda-derecha multiplicando el valor x por -1:



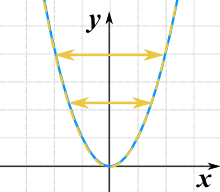
g(x) = (-x)2

¡Realmente lo voltea a la izquierda y a la derecha! Pero no se ve, porque x2 es simétrico respecto al eje y. Así que aquí tenemos otro ejemplo usando √(x):



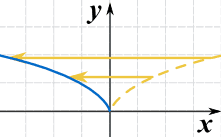
g(x) = √(-x)

Esto también se llama reflexión sobre el eje y-eje (el eje donde x=0)

Resumen

y = f(x) + C	C > 0 lo mueve hacia arriba C < 0 lo mueve hacia abajo
y = f(x + C)	C > 0 lo mueve hacia la izquierda C < 0 lo mueve a la derecha
y = Cf(x)	C > 1 lo estira en la y-dirección 0 < C < 1 lo comprime .
y = f(Cx)	C > 1 lo comprime en la x-dirección 0 < C < 1 lo estira	y = -f(x)	Lo refleja sobre el eje x-eje
y = f(-x)	La refleja sobre el eje y

Ejemplos

Ejemplo: la función g(x) = 1/x

Aquí tenemos algunas cosas que podemos hacer:

Mover 2 espacios hacia arriba:h(x) = 1/x + 2

Mover 3 espacios hacia abajo:h(x) = 1/x – 3

Mover 4 espacios hacia la derecha:h(x) = 1/(x-4) gráfico

Mover 5 espacios hacia la izquierda:h(x) = 1/(x+5)

Estíralo 2 en la dirección y:h(x) = 2/x

Comprímelo 3 en la dirección x:h(x) = 1/(3x)

Dale la vuelta:h(x) = -1/x

Ejemplo: la función v(x) = x3 – 4x

Aquí tenemos algunas cosas que podemos hacer:

Mover 2 espacios hacia arriba:w(x) = x3 – 4x + 2

Mover 3 espacios hacia abajo:w(x) = x3 – 4x – 3

Mover 4 espacios hacia la derecha:w(x) = (x-4)3 – 4(x-4)

Mueve 5 espacios a la izquierda:w(x) = (x+5)3 – 4(x+5) gráfico

Estira 2 en la dirección y:w(x) = 2(x3 – 4x)
= 2×3 – 8x

Comprime en 3 en la dirección x:w(x) = (3x)3 – 4(3x)
= 27×3 – 12x

Dale la vuelta:w(x) = -x3 + 4x

Todo en uno … !

Podemos hacer toda la transformación de una sola vez usando esto:



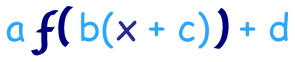
a es el estiramiento/compresión vertical

• |a| > 1 estira
• .
• |a| < 1 comprime
• a < 0 invierte el gráfico hacia abajo

b es estiramiento/compresión horizontal

• |b| > 1 comprime
• |b| < 1 estira
• b < 0 invierte el gráfico a la izquierda-derecha

c es el desplazamiento horizontal

• c < 0 desplaza a la derecha
• c > 0 desplaza a la izquierda

d es el desplazamiento vertical

• d > 0 se desplaza hacia arriba
• d < 0 se desplaza hacia abajo

.