Um teste t independente de duas amostras pode ser executado com base em dados de amostra de uma variável de resultado numérico normalmente distribuída para determinar se a sua média difere entre dois grupos independentes. Por exemplo, poderíamos ver se a média de GPA difere entre os calouros e os estudantes do ensino superior, recolhendo uma amostra de cada grupo de estudantes e registando os seus GPAs.
Hypotheses:
Ho: A média populacional de um grupo é igual à média populacional do outro grupo, ou μ1 = μ2
HA: A média populacional de um grupo não é igual à média populacional do outro grupo, ou μ1 ≠ μ2
Este teste também pode ser conduzido com uma hipótese alternativa direccional:
Ho: A média populacional de um grupo é igual à média populacional do outro grupo, ou μ1 = μ2
Ha: A média populacional de um grupo é maior que a média populacional do outro grupo, ou μ1 > μ2
A estatística do teste para um teste t independente de duas amostras é calculada tomando a diferença nas duas médias da amostra e dividindo pelo erro padrão estimado, combinado ou não. O erro padrão estimado é uma medida agregada da quantidade de variação em ambos os grupos.
Equações Relevantes:
Graus de liberdade: Varia por condições, mas a regra básica para cálculos manuais é a menor de n1 – 1 e n2 – 1, onde n é o tamanho da amostra para cada grupo.
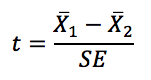
Assumptions:
- Amostras aleatórias
- Observações independentes
- A população de cada grupo é normalmente distribuída.
- As variações da população são iguais.
Se a terceira suposição não for cumprida, o teste alternativo é o teste Mann-Whitney U-Test, que pode ser executado para ver se existe uma diferença entre dois grupos para uma variável com qualquer tipo de distribuição.
Se a quarta suposição for cumprida, então o erro-padrão estimado do conjunto é utilizado no cálculo da estatística do teste. Se a quarta hipótese falhar, então o erro padrão estimado estimado mais conservador é utilizado (e o teste é referido como “Welch’s Test”).
Exemplo 1: Vídeo de cálculo manual
Este exemplo analisa o número médio de horas de sono para os estudantes do sexo masculino versus feminino.


Amostras de conclusão: Com t(df=40)=1,73, que foi mais extremo do que o nosso valor crítico de 1,68, estes dados fornecem provas de que as estudantes femininas dormem mais, em média, do que os estudantes masculinos.
Exemplo 2: Como correr em Excel 2016
Algumas destas análises requerem que tenha o add-in Data Analysis ToolPak em Excel activado. Para instruções sobre como realizar esta análise em versões anteriores do Excel, visite https://stat.utexas.edu/videos
Neste tutorial, irá determinar se os homens e as mulheres diferem no seu nível de felicidade.
NOTE: Neste vídeo, o teste t é realizado assumindo variações desiguais (Welch’s Test).
P>Conjunto de dados utilizado no vídeo
Direcções PDF correspondentes ao vídeo

>p>Conclusão da amostra: Com t(df=28)=2,29, p<0,05, estes dados fornecem provas de que as estudantes do sexo feminino são, em média, mais felizes do que os estudantes do sexo masculino.
Exemplo 3: Como correr no RStudio
Este exemplo analisa o número médio de horas de sono para estudantes do sexo masculino versus feminino.
NOTE: Neste vídeo, o teste t é realizado assumindo variações desiguais (Welch’s Test).
Dataset usado no vídeo
R ficheiro de script usado no vídeo

Conclusão da amostra: Com t(df=27)=-0.42, p>0.05, não encontramos evidências que sugiram que os estudantes masculinos e femininos dormem quantidades diferentes, em média, nas noites de terça-feira.