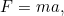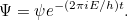Schrödingers equação – o que é?

Aqui está uma pergunta típica de um livro de texto. O seu carro ficou sem gasolina. Com quanta força é necessário empurrá-lo para o acelerar a uma determinada velocidade?

A resposta vem da segunda lei do movimento de Newton:

>>

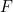onde é aceleração, é força e 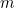é massa. Esta lei maravilhosamente simples, mas subtil, permite-lhe descrever movimentos de todos os tipos e por isso pode, pelo menos em teoria, responder a praticamente qualquer pergunta que um físico possa querer fazer sobre o mundo.

Or pode? Quando as pessoas começaram a considerar o mundo pela primeira vez nas escalas mais pequenas, por exemplo os electrões que orbitam o núcleo da anatomia, aperceberam-se de que as coisas se tornam realmente muito estranhas e que as leis de Newton já não se aplicam. Para descrever este mundo minúsculo é necessária uma mecânica quântica, uma teoria desenvolvida no início do século XX. A equação central desta teoria, a análoga da segunda lei de Newton, chama-se equação de Schrödinger.

Ondas e partículas

“Na mecânica clássica descrevemos um estado de um sistema físico usando posição e impulso”, explica Nazim Bouatta, um físico teórico da Universidade de Cambridge. Por exemplo, se tiver uma mesa cheia de bolas de bilhar em movimento e souber a posição e o momento (que é a massa vezes a velocidade) de cada bola em algum momento 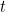, então sabe tudo o que há para saber sobre o sistema nesse momento 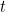: onde tudo está, onde tudo está a ir e a que velocidade. “O tipo de pergunta que então fazemos é: se conhecemos as condições iniciais de um sistema, ou seja, conhecemos o sistema na altura 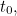qual é a evolução dinâmica deste sistema? E para isso utilizamos a segunda lei de Newton. Na mecânica quântica fazemos a mesma pergunta, mas a resposta é complicada porque a posição e o impulso já não são as variáveis certas para descrever”.

O problema é que os objectos que a mecânica quântica tenta descrever nem sempre se comportam como pequenas bolinhas de bilhar. Por vezes é melhor pensar neles aswaves. “Tomemos o exemplo da luz. Newton, para além do seu trabalho sobre gravidade, também estava interessado na óptica”, diz Bouatta. “De acordo com Newton, a luz era descrita por partículas. Mas então, após o trabalho de muitos cientistas, incluindo o entendimento teórico fornecido por James Clerk Maxwell, descobrimos que a luz era descrita por ondas”

Mas em 1905 Einstein percebeu que a imagem da onda também não era inteiramente correcta. Para explicar o efeito fotoeléctrico (ver o artigo Plus crise de identidade da Luz)é preciso pensar num feixe de luz como um fluxo de partículas, que Einstein apelidou de fótons. O número de fotões é proporcional à intensidade da luz, e a energia E de cada fotão é proporcional à sua frequência f:

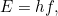Aquié a constante de Planck, um número incrivelmente pequeno com o nome do físico Max Planck que já tinha adivinhado esta fórmula em 1900 no seu trabalho sobre a radiação do corpo negro.”Então estávamos perante uma situação em que por vezes a forma correcta de describinglight era como ondas e por vezes como partículas”, diz Bouatta.

O resultado de Einstein ligado ao antigo esforço, iniciado no século XVII por Christiaan Huygens e explorado novamente no século XIX por William Hamilton: para unificar a física da óptica (que era tudo sobre ondas) e a mecânica (que era tudo sobre partículas). Inspirado pelo comportamento esquizofrénico da luz, o jovem físico francês Louis deBroglie deu um passo dramático nesta viagem: postulou que não só a luz, mas também a matéria sofria da chamada dualidade onda-partícula. Os minúsculos blocos de construção da matéria, como os electrões, também se comportam como partículas em algumas situações e como ondas noutras.

A ideia de Broglie, que ele anunciou na década de 1920, não se baseava em provas experimentais, mas sim em considerações teóricas inspiradas na teoria da relatividade de Einstein. Mas as provas experimentais logo se seguiram. No final da década de 1920, experiências envolvendo partículas espalhadas por um cristal confirmaram a natureza ondulatória dos electrões (ver o artigo Plus, Incerteza Quântica).

Uma das demonstrações mais famosas da dualidade onda-partícula é a experiência da dupla fenda. Nela os electrões (ou outras partículas como fotões ou neutrões) são disparados um de cada vez sobre um ecrã contendo duas fendas. Atrás do ecrã há um segundo que pode detectar onde vão parar os electrões que passaram pelas fendas. Se os electrões se comportassem como partículas, então seria de esperar que se amontoassem em torno de duas linhas rectas atrás das duas fendas. Mas o que se vê realmente no ecrã do detector é um padrão de interferência: o padrão que se obteria se os electrões fossem ondas, cada onda passando por ambas as fendas ao mesmo tempo e depois interferindo consigo própria à medida que se espalha novamente pelo outro lado. No entanto, no ecrã do detector, os electrões são registados como chegando, tal como seria de esperar: como partículas. É de facto um resultado muito estranho, mas que já foi replicado muitas vezes – temos simplesmente de aceitar que esta é a forma como o mundo funciona.

equação de Schrödinger

A nova imagem radical proposta por de Broglie exigia uma nova física. Como é que uma onda associada a uma partícula se parece matematicamente? Einstein já tinha relacionado a energia 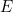de um fotão com a frequência 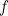de luz, que por sua vez está relacionada com o comprimento de onda 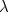pela fórmula 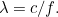Aqui é a velocidade da luz. Usando resultados da teoria da relatividade é também possível relacionar a energia de um fóton com o seu impulso. Juntando tudo isto dá a relação

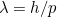
entre o comprimento de onda do fóton 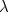e momentum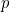 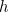de novo é a constante de Planck).

(Ver crise de identidade da Luz para detalhes.)

Seguir a partir disto,de Broglie postulou que a mesma relação entre o comprimento de onda e o momento deve manter-se para qualquer partícula.

Neste ponto, é melhor suspender a sua intuição sobre o que realmente significa dizer que uma partícula se comporta como uma onda (veremos isso no terceiro artigo)e apenas seguir em frente com a matemática.

Na mecânica clássica a evolução no tempo de uma onda, por exemplo uma onda sonora ou uma onda aquática, é descrita por uma equação de onda: uma equação diferencial cuja solução é uma função de onda, que lhe dá a forma da onda em qualquer altura 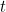(sujeito a condições de contorno adequadas).

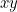Por exemplo, suponha que tem ondas a viajar através de um cordel que é esticado ao longo do -eixo e vibra no -plano. Para descrever completamente a onda, é necessário encontrar o deslocamento 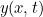da corda no 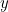-direcção em cada ponto e cada vez 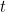. Usando a segunda lei do movimento de Newton é possível mostrar que 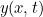obedece à seguinte equação da onda:

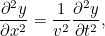where é a velocidade das ondas.

Uma solução geral 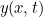a esta equação é bastante complicada, reflectindo o facto de que a corda pode estar a oscilar de todas as maneiras, e que é necessário mais informação (condições iniciais e condições de contorno) para descobrir exactamente que tipo de movimento é. Mas como exemplo, a função

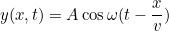descreve uma onda a viajar no positivo -direcção com uma frequência angular 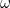, por isso, como seria de esperar, é uma solução possível para a equação da onda.

Por analogia, deveria haver uma equação de onda que regesse a evolução das misteriosas “ondas de matéria”, sejam elas quais forem, ao longo do tempo. A sua solução seria uma função de onda 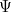(mas resista a pensar nela como descrevendo uma onda real) que lhe diz tudo o que há para saber sobre o seu sistema quântico – por exemplo, uma única partícula a mover-se numa caixa – em qualquer altura 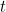. Foi o físico austríaco Erwin Schrödinger que inventou esta equação em 1926. Para uma única partícula em movimento em três dimensões, a equação pode ser escrita como

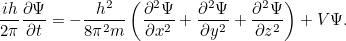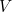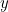
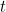
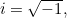
aqui é a energia potencial da partícula (uma função de e 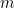é a massa da partícula e 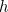é a constante de Planck. A solução para esta equação é a função de onda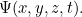

em algumas situações a energia potencial não depende do tempo 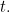Neste caso, podemos frequentemente resolver o problema considerando a versão mais simples, independente do tempo, da equação de Schrödinger para uma função 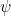dependendo apenas do espaço, i.e.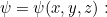

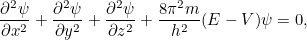onde 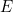é a energia total da partícula. A solução 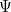à equação completa é então

Estas equações aplicam-se a uma partícula em movimento em três dimensões, mas têm contrapartes que descrevem um sistema com qualquer número de partículas. E em vez de formular a função de onda em função da posição e do tempo, também se pode formulá-la em função do impulso e do tempo.

Entrar incerteza

Veremos como resolver a equação de Schrödinger para um exemplo simples no segundo artigo, e também que a sua solução é de facto semelhante à equação matemática que descreve uma onda.

Mas o que é que esta solução realmente significa? Não lhe dá uma localização precisa da sua partícula num dado momento 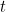, por isso não lhe dá a trajectória de uma partícula ao longo do tempo. É antes uma função que, num dado momento 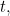lhe dá um valor 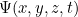para todos os locais possíveis 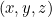. O que significa este valor? Em 1926, o físico Max Born inventou uma interpretação probabilística. Ele postulou que o quadrado do valor absoluto da função da onda,

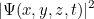dá-lhe a densidade de probabilidade de encontrar a partícula na posição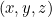no momento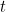. Por outras palavras, a probabilidade de a partícula ser encontrada numa região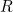no momento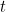é dada pela integral

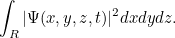(Pode saber mais sobre densidades de probabilidade em qualquer introdução à teoria da probabilidade, por exemplo, aqui.)

Esta imagem probabilística liga-se a uma consequência bastante chocante da fórmula de de Broglie para o comprimento de onda e o impulso de uma partícula, descoberta por Werner Heisenberg em 1927. Heisenberg descobriu que existe um limite fundamental para a precisão a que se pode medir a posição e o momento da partícula amovível. Quanto mais preciso se quiser ser sobre uma, menos se pode dizer sobre a outra. E isto não se deve à qualidade do seu instrumento de medição, mas sim a uma incerteza de natureza fundamental. Este resultado é agora conhecido como o princípio de incerteza de Heisenberg e é um dos resultados que é frequentemente citado para ilustrar a estranheza da mecânica quântica. Significa que na mecânica quântica simplesmente não podemos falar sobre a localização ou a trajectória de uma partícula.

“Se acreditamos neste quadro de incerteza, então temos de aceitar um relato probabilístico porque não temos respostas exactas a perguntas como ‘onde está o electrão no momento 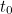?”,” diz Bouatta. Por outras palavras, tudo o que se pode esperar da representação matemática de um estado quântico, da função de onda, é que isso lhe dê uma probabilidade.

Se a função de onda tem ou não qualquer interpretação física foi e continua a ser uma questão delicada. “A questão era, temos esta função de onda, mas será que estamos realmente a pensar que há ondas a proliferar no espaço e no tempo?” diz Bouatta. “De Broglie, Schrödinger e Einstein weretrying para fornecer um relato realista, que é como uma onda de luz, por exemplo, a propagar-se no vácuo. Mas , Wolfgang Pauli, Werner Heisenberg e Niels Bohr estavam contra este quadro realista. Para eles, a função de onda era apenas uma ferramenta para computar probabilidades”. Vamos ver mais de perto a interpretação da função de onda no terceiro artigo desta série.

Funciona?

Por que devemos acreditar neste cenário bastante fantástico? Neste artigo apresentámos a equação de Schrödinger como se fosse arrancada do ar, mas de onde é que ela vem realmente? Como é que Schrödingerderder a conseguiu? O famoso físico Richard Feynman considerou esta questãofutilante: “De onde é que o obtivemos? Não é possível derivar de qualquer coisa que se saiba. Saiu-lhes da mente de Schrödinger”.

Yet, a equação manteve-se em todas as experiências até agora. “É a equação maisfundamental da mecânica quântica”, diz Bouatta. “É o ponto de partida para cada sistema de mecânica quântica que queremos descrever:electrões, prótons, neutrões, o que quer que seja”. O sucesso mais procurado da equação, que foi também uma das motivações de Schrödinger, foi descrever um fenómeno que tinha ajudado a dar origem à mecânica quântica em primeiro lugar: o discreto espectro de energia do átomo de hidrogénio. Segundo o modelo satómico de Ernest Rutherford, a frequência da radiação emitida por átomos como o hidrogénio deveria varycontinuamente. As experiências mostraram, contudo, que não: o átomo de hidrogénio só emite radiação em certas frequências, há um salto quando a frequência muda. Esta descoberta voou em face da sabedoria convencional, que endossou uma máxima estabelecida pelo filósofo e matemático do século XVII Gottfried Leibniz: “a natureza não faz saltos”.

Em 1913, Niels Bohr apresentou um novo modeloatómico no qual os electrões estão restritos a certos níveis de energia. Schrödinger aplicou a sua equação à hidrogenatom e descobriu que as suas soluções reproduziam exactamente os níveis de energia estimulados por Bohr. “Este foi um resultado espantoso – e um dos primeiros grandes êxitos da equação de Schrödinger”, diz Bouatta.

Com inúmeros sucessos experimentais sob o seu cinto, a equação de Schrödinger tornou-se o análogo estabelecido da segunda lei de movimento de Newton para a mecânica quântica. Agora vejamos a equação de Schrödinger em acção, usando o exemplo simples de uma partícula a mover-se numa caixa. Vamos também explorar outra estranha consequência da equação chamada tunelização quântica.

Leia o próximo artigo: Equação de Schrödinger – em acção
Mas se não lhe apetecer fazer as contas pode saltar directamente para o terceiro artigo que explora a interpretação da função da onda.

Sobre este artigo

Nazim Bouatta é um Pós-Doutorado em Fundamentos da Física na Universidade de Cambridge.

Marianne Freiberger é editora da Plus. Ela entrevistou Bouatta em Cambridge em Maio de 2012. Ela também gostaria de agradecer a Jeremy Butterfield, filósofo de física da Universidade de Cambridge, e a Tony Short, um Fellow de Investigação da Royal Society em Fundações da Física Quântica na Universidade de Cambridge, pela sua ajuda na redacção destes artigos.