Expansões Binomiais Utilizando o Triângulo de Pascal
Considerar os seguintes poderes expandidos de (a + b)n, onde a + b é qualquer binómio e n é um número inteiro. Procure padrões.
br>>A cada expansão é um polinómio. Há alguns padrões a serem observados.
1. Há mais um termo do que o poder do expoente, n. Ou seja, há termos na expansão de (a + b)n.
2. Em cada termo, a soma dos expoentes é n, o poder ao qual o binómio é elevado.
3. Os expoentes de um início com n, o poder do binómio, e diminuem para 0. O último termo não tem factor de a. O primeiro termo não tem factor de b, portanto as potências de b começam com 0 e aumentam para n.
4. Os coeficientes começam com 1 e aumentam através de certos valores cerca de “metade” – de forma e depois diminuem através destes mesmos valores de volta para 1.
Vamos explorar os coeficientes mais a fundo. Suponhamos que queremos encontrar uma expansão de (a + b)6. Os padrões que acabámos de observar indicam que existem 7 termos na expansão:
a6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6.
Como podemos determinar o valor de cada coeficiente, ci? Podemos fazê-lo de duas maneiras. O primeiro método envolve a escrita dos coeficientes numa matriz triangular, como se segue. Isto é conhecido como o triângulo de Pascal: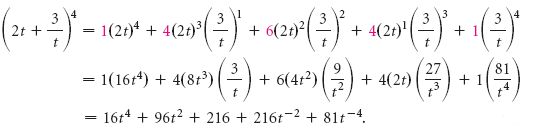
há muitos padrões no triângulo. Encontre tantos quantos puder.
Talvez tenha descoberto uma forma de escrever a próxima fila de números, dados os números na fila acima dela. Há sempre 1’s no exterior. Cada número restante é a soma dos dois números acima dele. Vamos tentar encontrar uma expansão para (a + b)6, adicionando outra linha usando os padrões que descobrimos:
br>> vemos que na última linha
p>os 1º e último números são 1;
o 2º número é 1 + 5, ou 6;
o 3º número é 5 + 10, ou 15;
o 4º número é 10 + 10, ou 20;
o 5º número é 10 + 5, ou 15; e
o 6º número é 5 + 1, ou 6.p>Assim a expansão para (a + b)6 é
(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Para encontrar uma expansão para (a + b)8, completamos mais duas filas do triângulo de Pascal: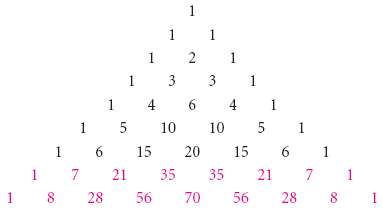
br>Assim a expansão de é
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Podemos generalizar os nossos resultados da seguinte forma.
O Teorema Binomial Usando o Triângulo de Pascal
Para qualquer binómio a + b e qualquer número natural n,
(a + b)n = c0anb0 + c1an-1b1 + c2an-2b2 + …. + cn-1a1bn-1 + cna0bn,
onde os números c0, c1, c2,…., cn-1, cn são da (n + 1)-primeira fila do triângulo de Pascal.
Exemplo 1 Expandir: (u – v)5.
Solução Temos (a + b)n, onde a = u, b = -v, e n = 5. Utilizamos a 6ª fila do triângulo de Pascal:
1 5 10 10 5 1
Então temos
(u – v)5 = 5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5.
Nota que os sinais dos termos alternam entre + e -. Quando o poder de -v é estranho, o sinal é -.
Exemplo 2 Expandir: (2t + 3/t)4.
Solução Temos (a + b)n, onde a = 2t, b = 3/t, e n = 4. Usamos a 5ª fila do triângulo de Pascal:
1 4 6 4 1
Então temos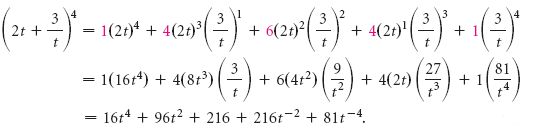
Expansão cinomial usando a Notação Factorial
P>Ponhamos que queremos encontrar a expansão de (a + b)11. A desvantagem na utilização do triângulo de Pascal é que devemos calcular todas as linhas anteriores do triângulo para obter a linha necessária para a expansão. O método seguinte evita isto. Também nos permite encontrar um termo específico – digamos, o 8º termo – sem calcular todos os outros termos da expansão. Este método é útil em cursos como matemática finita, cálculo e estatística, e utiliza a notação do coeficiente binomial 
.
Podemos restabelecer o teorema binomial como se segue.
The Binomial Theorem Using Factorial Notation
For any binomial (a + b) and any natural number n,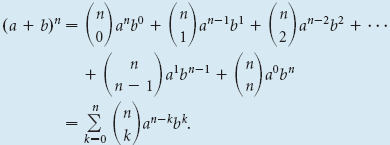
.
O teorema binomial pode ser provado por indução matemática. (VerExercise 63.) Este formulário mostra porque é chamado coeficiente binomial.
Exemplo 3 Expandir: (x2 – 2y)5.
Solução Temos (a + b)n,onde a = x2, b = -2y, e n = 5. Depois utilizando o teorema binomial, temos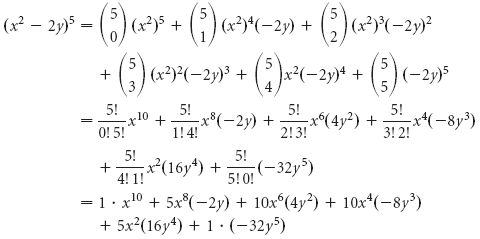
Finalmente (x2 – 2y)5 = x10 – 10x8y + 40x6y2 – 80x4y3 + 80x2y4 – 32y5.
Examplo 4 Expandir: (2/x + 3√x)4.
Solução Temos (a + b)n, onde a = 2/x, b = 3√x, e n = 4. Depois, utilizando o teorema binomial, temos
br>Finalmente (2/x + 3√x)4 = 16/x4 + 96/x5/2 + 216/x + 216×1/2 + 81×2.
Finding a Specific Term
P>Ponhamos que queremos determinar apenas um termo particular de uma expansão. O método que desenvolvemos permitir-nos-á encontrar tal termo sem calcular todas as filas do triângulo de Pascal ou todos os coeficientes precedentes.
Nota que no teorema binomial, 
nos dá o 1º termo, 
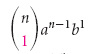nos dá o 2º termo, 
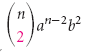nos dá o 3º termo, e assim por diante. Isto pode ser generalizado da seguinte forma.
Encontrar o (k + 1)-st termo
O (k + 1)-st termo de (a + b)n é 
.
Exemplo 5 Encontrar o 5º termo na expansão de (2x – 5y)6.
Solução Primeiro, notamos que 5 = 4 + 1. Assim, k = 4, a = 2x, b = -5y, e n = 6. Depois o 5º termo da expansão é
Exemplo 6 Encontrar o 8º termo na expansão de (3x – 2)10.
Solução Primeiro, notamos que 8 = 7 + 1. Assim, k = 7, a = 3x, b = -2, e n = 10. Depois o 8º termo da expansão é
Número total de subconjuntos
Suponha que um conjunto tem n objectos. O número de subconjuntos contendo k elementos . O número total de subconjuntos de um conjunto é o número de subconjuntos com 0 elementos, mais o número de subconjuntos com 1 elemento, mais o número de subconjuntos com 2 elementos, e assim por diante. O número total de subconjuntos de um conjunto com n elementos é
.
br>Agora considere a expansão de (1 + 1)n:
.
Assim, o número total de subconjuntos é (1 + 1)n, ou 2n. Provámos o seguinte.
Número total de subconjuntos
O número total de subconjuntos de um conjunto com n elementos é 2n.
Exemplo 7 O conjunto {A, B, C, D, E} tem quantos subconjuntos?
Solução O conjunto tem 5 elementos, pelo que o número de subconjuntos é 25, ou 32.
Exemplo 8 Wendy’s, uma cadeia nacional de restaurantes, oferece os seguintes toppings para os seus hambúrgueres:
{catsup, mostarda, maionese, tomate, alface, cebola, picles, sabor, queijo}.
Quantos tipos diferentes de hambúrgueres a Wendy’s pode servir, excluindo o tamanho do hambúrguer ou o número de coberturas?
p>Solução As coberturas em cada hambúrguer são os elementos de um subconjunto de todas as coberturas possíveis, sendo o conjunto vazio um hambúrguer simples. O número total de hambúrgueres possíveis é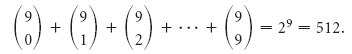
br>>Então Wendy’s serve hambúrgueres de 512 maneiras diferentes.