p>Voltar ao Índice de Lições | Fazer as Lições por Ordem | Página de fácil impressão
p> Funções Exponenciais: Interesse Composto (página 4 de 5)
Seções: Introdução, Avaliação, Gráficos, Interesse Composto, O exponencial natural
Uma equação exponencial muito importante é a fórmula de interesse composto:
![]()
…onde “A” é o montante final, “P” é o montante inicial (ou “principal”), “r” é a taxa de juro (expressa como decimal), “n” é o número de compostos por ano, e “t” é o número total de anos.
P>P>Para as variáveis, n refere-se ao número de compostos em qualquer ano, não ao número total de compostos ao longo da vida do investimento. Se os juros são compostos anualmente, então n = 1; se semestralmente, então n = 2; trimestralmente, então n = 4; mensalmente, então n = 12; semanalmente, então n = 52; diariamente, então n = 365; e assim por diante, independentemente do número de anos envolvidos. Além disso, “t” deve ser expresso em anos, porque as taxas de juro são expressas dessa forma. Se um exercício afirma que o capital foi investido por seis meses, seria necessário convertê-lo para 6/12 = 0,5 anos; se foi investido por 15 meses, então t = 15/12 = 1,25 anos; se foi investido por 90 dias, então t = 90/365 de um ano; e assim por diante.
Nota que, para uma dada taxa de juro, a fórmula acima simplifica para a simples forma exponencial a que estamos habituados. Por exemplo, que a taxa de juro r seja de 3%, composta mensalmente, e que o montante inicial do investimento seja de $1250. Depois a equação de juros compostos, para um período de investimento de t anos, torna-se:
![]()
…onde a base é 1.0025 e o expoente é a expressão linear 12t.
para fazer problemas de palavras de interesse composto, geralmente a única parte difícil é descobrir quais os valores que vão para onde na fórmula de interesse composto. Uma vez que todos os valores estejam devidamente ligados, é possível resolver para qualquer variável que sobrar.
Advertisement
- Ponha que planeia precisar de $10.000 dentro de trinta e seis meses, quando o seu filho começar a frequentar a universidade. Deseja investir num instrumento que rende 3,5% de juros, compostos mensalmente. Quanto deve investir?
Para resolver isto, tenho de descobrir que valores combinam com que variáveis. Neste caso, quero acabar com $10.000, portanto A = 10.000. A taxa de juro é de 3,5%, portanto, expressa como decimal, r = 0,035. O prazo é de trinta e seis meses, portanto t = 36/12 = 3. E os juros são compostos mensalmente, pelo que n = 12. A única variável restante é P, que representa o quanto comecei. Uma vez que estou a tentar descobrir quanto investir em primeiro lugar, então resolver para P faz sentido. Vou ligar todos os valores conhecidos, e depois vou resolver para a variável restante:
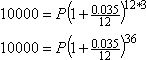
A tentação neste ponto é simplificar no lado direito, e depois dividir para resolver para P. Não faça isso; tende para o erro de arredondamento, e pode causar-lhe problemas mais tarde. Em vez disso, mantenha-se exacto, e faça a divisão simbolicamente (e exactamente) primeiro:
![]()
Agora vou fazer toda a simplificação na minha calculadora, trabalhando de dentro para fora, para que tudo seja levado na memória e eu obtenha a resposta mais exacta possível:

P>Eu preciso de investir cerca de $9004.62.
(O problema não especificava como arredondar, mas neste caso, não precisava de o fazer. Os problemas de dólares e cêntimos arredondam-se sempre a duas casas decimais). Copyright © Elizabeth Stapel 2002-2011 Todos os direitos reservados
Deverá memorizar a fórmula de juros compostos, mas deverá também memorizar o significado de cada uma das variáveis da fórmula. Embora lhe possa ser dada a fórmula no teste, é improvável que lhe sejam dados os significados das variáveis, e, sem os significados, não será capaz de completar os exercícios.
<< Previous Top | 1 | 2 | 2 | 3 | 4 | 5 | Return to Index Next >>
|
Cite este artigo como: |
Stapel, Elizabeth. “Funções Exponenciais”: Compound Interest”. Purplemath. Disponível de 2016
|