
/div>
/div>
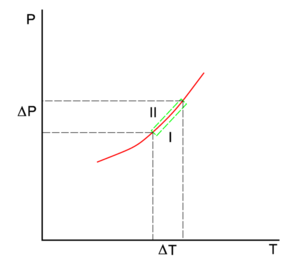
A linha vermelha no diagrama P-T é a curva de coexistência de duas fases, I e II, de um sistema de um único componente. A fase I pode ser o vapor e a II a fase líquida do componente. A linha verde inferior dá a inclinação na fase I e a linha verde superior na fase II.
A relação Clausius-Clapeyron é uma equação para um sistema monocomponente que consiste em duas fases em equilíbrio termodinâmico a temperatura absoluta constante T e pressão constante P. Uma curva num diagrama termodinâmico bidimensional que separa duas fases em equilíbrio é conhecida como uma curva de coexistência. A relação Clausius-Clapeyron dá a inclinação da curva de coexistência no diagrama P-T:
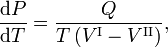
onde Q é o calor molar de transição. É o calor necessário para trazer uma toupeira do composto que constitui o sistema da fase II para a fase I; é também conhecido como calor latente. Para as transições de fase com P constante, é a entalpia de transição molar. Por exemplo, quando a fase II é um líquido e a fase I é um vapor, então Q ≡ Hv é o calor molar de vaporização (também conhecido como entalpia molar de evaporação). Além disso, V I é o volume molar da fase I à pressão P e temperatura T do ponto em que a inclinação é considerada e V II é o mesmo para a fase II.
A equação tem o nome de Émile Clapeyron, que a publicou em 1834, e Rudolf Clausius, que a colocou numa base termodinâmica firme em 1850.
>br>
Conteúdo
- 1 Derivação
- 2 Solução aproximada
- 3 Aplicação
- 4 Referência
Derivação
A condição de equilíbrio termodinâmico a pressão constante P e temperatura constante T entre duas fases I e II é a igualdade das energias livres de Gibbs molar G,
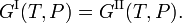
A energia livre de Gibbs molar da fase α (α = I, II) é igual ao químico potentialμα desta fase. Assim, a condição de equilíbrio pode ser escrita como,
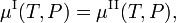
que se mantém em todo o lado ao longo da curva de coexistência (vermelha) na figura.
se formos reversivelmente ao longo da linha verde inferior e superior na figura , os potenciais químicos das fases, sendo funções de T e P, mudam por ΔμI e ΔμII, para as fases I e II, respectivamente, enquanto o sistema se mantém em equilíbrio,
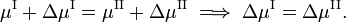
Da termodinâmica clássica sabe-se que
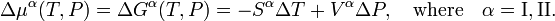
Aqui Sα é a entropia molar (entropia por molar) de phaseα e Vα é o volume molar (volume de uma molar) desta fase. Segue-se que
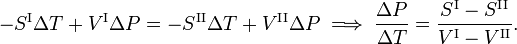
Da segunda lei da termodinâmica é sabido que para uma transição de fase reversível se mantém que
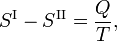
onde Q é a quantidade de calor necessária para converter uma toupeira da fase II em fase I. A eliminação da entropia e a tomada do limite de infinitesimamente pequenas alterações em T e P dá a equação de Clausius-Clapeyrone,
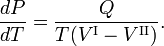
Solução aproximada
A equação de Clausius-Clapeyron é exacta. Quando são feitas as seguintes hipóteses, pode ser integrada:
- O volume molar da fase II é insignificante em comparação com o volume molar da fase I: V I >> V II. Em geral, longe do ponto crítico, esta desigualdade mantém-se bem para os equilíbrios líquido-gás.
- Fase I satisfaz a lei ideal do gás, onde R é a constante de gás molar,
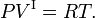 Se a fase I for um gás e a pressão for bastante baixa, esta suposição é razoável.
Se a fase I for um gás e a pressão for bastante baixa, esta suposição é razoável.
- A transição (latente) de calor Q é constante durante o intervalo de integração de temperatura. As integrações vão da temperatura inferior T1 para a temperatura superior T2 e de P1 para P2.
Até estas condições o Clausius-A equação de Clapeyron torna-se
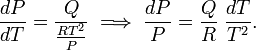
Integração dá
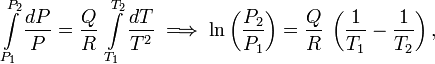
Aplicação
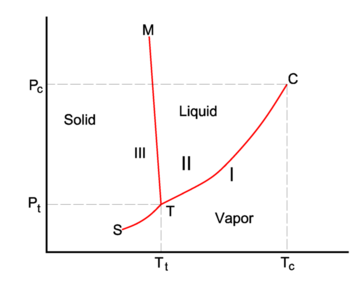
P-Diagrama T de água. Esquema e qualitativo.
Na figura à direita é mostrada uma impressão de parte do diagrama de fase da água (H2O). As três fases são: I (vapor), II (líquido) e III (sólido). A equação de Clausius-Clapeyron
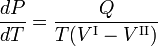
dá a inclinação das três curvas de coexistência (equilíbrio, vermelho). A linha de ebulição T-C tem uma inclinação positiva, porque o calor de vaporização Q = Hv é positivo e o volume molar do vapor V I é (muito) maior do que o do líquido V II. Por uma razão semelhante, a sublimação (transição do sólido para o vapor) da linha T-S tem um declive positivo. A linha de sublimação T-S é mais inclinada que a linha de ebulição T-C porque o calor da sublimação é maior que o calor da vaporização, enquanto que na vizinhança do ponto de passagem T (o ponto triplo) a diferença nos volumes molares é quase igual. A linha de fusão T-M tem um declive negativo, que ocorre apenas para alguns compostos (entre eles água). Considere
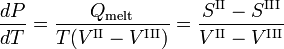
O volume molar VIII do sólido é maior do que o volume molar VII do líquido, enquanto a entalpia de fusão Qmelt = SII-SIII > 0 (um líquido tem uma entropia maior do que o sólido correspondente, custa energia para fundir um sólido). Compostos que têm linhas de fusão com inclinação negativa, têm uma fase sólida de menor densidade do que a fase líquida. Por exemplo, é muito conhecido que a água sólida (gelo) flutua sobre a água líquida.
O ponto C é o ponto crítico. Para além deste ponto, o vapor e o líquido são um fluido indistinguível. Não há transição de fase ou uma interface de fase à direita da linha de fusão e acima da linha da constante P = Pc. O fluido gás/líquido também aparece à direita da linha da constante T = Tc.
A relação Clausius-Clapeyron também se mantém para transições entre diferentes fases cristalinas.