A história da fundação da Microsoft é um dos episódios mais famosos da história da incomputação. Em 1975, Paul Allen voou para Albuquerque para demonstrar ao intérprete BASIC que ele e Bill Gates tinham escrito para o Altairmicrocomputador. Porque nenhum deles tinha um Altair, Allen e Gatestestestest, o seu intérprete, utilizando um emulador que tinham escrito e executado no sistema scomputer de Harvard. O emulador baseava-se em nada mais do que nas especificações publishedspecifications para o processador Intel 8080. Quando Allen finalmente correu o seu intérprete num verdadeiro Altair-in à frente da pessoa que ele e Gates esperavam comprar o seu software – ele não fazia ideia se iria funcionar. Mas funcionou. No mês seguinte, Allen e Gates fundaram oficialmente a sua nova empresa.
p>Até um século antes de Allen e Gates escreverem o seu intérprete BASIC, AdaLovelace escreveu e publicou um programa de computador. Também ela escreveu um programa fora do computador que só lhe tinha sido descrito. Mas o seu programa, ao contrário do intérprete BASIC da Microsoft, nunca foi executado, porque o computador a que ela se destinava nunca foi construído.
O programa de AdaLovelace é muitas vezes chamado o primeiro programa de computador do mundo. Note-se que toda a gente concorda que se deve chamar assim. O legado de Lovelace, acontece, é um dos temas mais debatidos da história da computação. Walter Isaacson escreveu que a disputa sobre a extensão e o mérito da sua contribuição constitui uma “especialidade académica menor “1. Inevitavelmente, o facto de Lovelace ter sido uma mulher fez desta disputa uma disputa carregada. Os historiadores têm citado todos os tipos de provas primárias para argumentar que o crédito dado a Lovelace é apropriado ou não merecido. Mas parecem passar menos tempo a explicar os detalhes técnicos da sua escrita publicada, o que é lamentável, porque os detalhes técnicos são a parte mais fascinante da história. Quem não gostaria de saber exactamente como é que um programa escrito em 1843 deveria funcionar?
Em justiça, o programa de Lovelace não é fácil de explicar ao leigo com um grande aceno de mão. São os meandros do seu programa, no entanto, que o tornam lamentável. Se ela deveria ou não ser conhecida como “a primeira programadora”, o seu programa foi especificado com um grau de rigor que ultrapassou de longe tudo o que já tinha acontecido antes. Ela pensou cuidadosamente sobre como as operações poderiam ser organizadas em grupos que pudessem ser repetidas, inventando assim o laço. Percebeu a importância de acompanhar o estado das variáveis à medida que mudavam, introduzindo a anotação para ilustrar essas mudanças. Como programadora, assustei-me com o quanto do que Lovelace estava a fazer se assemelhava à experiência de escrever software hoje.
Por isso, vamos dar uma olhada mais atenta ao programa de Lovelace. Ela concebeu-o para calcular os números de Bernoulli. Para compreender o que são, temos de recuar milénios até à génese de um dos problemas mais antigos da matemática.
Somas de Poderes
Os pitagóricos viviam nas margens do Mediterrâneo e adoravam os números. Um dos seus passatempos era fazer triângulos de seixos.

Um calhau seguido por uma fila de dois calhaus faz um triângulo contendo três seixos. Adiciona-se outra fileira de três seixos e obtém-se um triângulo contendo seis seixos. Pode continuar assim, adicionando cada vez uma fila com mais um calhau a mais do que a fila anterior. Um triângulo com seis seixos contém 21 seixos. Mas quantos seixos é que um triângulo com 423 seixos contém?
O que os pitagóricos procuravam era uma forma de calcular o seguinte, sem fazer toda a adição:
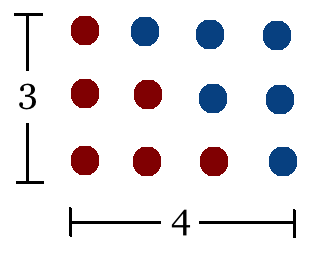
p>Acabaram por perceber que, se colocarmos dois triângulos do mesmo tamanho um contra o outro de modo a formar um rectângulo, podemos encontrar a área do rectângulo e dividir por dois para obter o número de seixos em cada um dos triângulos:
\p>Arquimedes explorou mais tarde um problema semelhante. Ele estava interessado nas seguintes séries:\\p>p>p>p>p>pode visualizar esta série imaginando uma pilha de quadrados progressivamente maiores (feitos de cubos minúsculos), um em cima do outro, formando uma pirâmide.Arquimedes queria saber se havia uma maneira fácil de dizer quantos cubos seriam necessários para construir uma pirâmide com, digamos, 423 níveis. Ele registou uma solução que também permite uma interpretação geométrica.2
Três pirâmides podem ser encaixadas para formar um prisma rectangular com uma extrusão minúscula, de um cubo-alto numa extremidade. Acontece que essa pequena extrusão é um atriângulo que obedece às mesmas regras que os pitagóricos utilizavam para fazer os seus triângulos de vértice. (Este videomight é uma explicação mais útil do que eu quero dizer.) Assim, o volume da forma bruta é dado pela seguinte equação:
\p>p> Substituindo a equação pitagórica pela soma dos primeiros nintegrantes e fazendo alguma álgebra, obtém-se isto:\\p> Em 499, o matemático e astrónomo indiano, Aryabhata, publicou uma obra conhecida como a Aryabhatiya, que incluía uma fórmula para calcular a soma de cubos:\p> Uma fórmula para a soma dos primeiros n inteiros positivos elevados à quarta potência não foi publicada durante mais 500 anos.3
Neste momento pode estar a perguntar-se se existe um método geral para encontrar a soma dos primeiros n inteiros elevados ao kth power.Os matemáticos também se estavam a perguntar. Johann Faulhaber, um matemático alemão e um numerólogo muito excêntrico, conseguiu calcular fórmulas para somas de inteiros até à 17ª potência, que publicou em 1631. Mas isto pode tê-lo levado anos e ele não declarou uma solução geral.4 Blaise Pascalfinalmente delineou um método geral em 1665, embora dependesse do primeiro conhecimento para calcular a soma de inteiros elevada a cada poder menor.5 Tocalculando a soma dos primeiros n inteiros positivos elevados à sexta potência, por exemplo, teria primeiro de saber calcular a soma dos primeiros n inteiros positivos elevados à quinta potência.
Uma solução geral mais prática foi declarada na obra publicada postumamente do matemático suíço Jakob Bernoulli, que morreu em 1705. Bernoulli começou a calcular as fórmulas de cálculo das somas dos primeiros n inteiros positivos ao primeiro, segundo e terceiro poderes.6 Estes ele deu forma inpolinomial, de modo que se pareciam com os seguintes:
\\p>Utilizando o Triângulo de Pascal, Bernoulli percebeu que estes polinómios seguiam um padrão previsível. Essencialmente, Bernoulli dividiu os coeficientes de eachterm em dois factores, um dos quais podia determinar usando o Triângulo de Pascal e o outro que podia derivar da propriedade interessante que todos os coeficientes no polinómio pareciam sempre acrescentar a um. A determinação do expoente que deveria estar ligado a cada termo não foi problema, porque isso também seguiu um padrão previsível. O factor de cada coeficiente que tinha de ser calculado utilizando a regra da soma em um formou uma sequência que ficou conhecida como os números de Bernoulli.
A descoberta de Bernoulli não significava que fosse agora trivial calcular a soma dos primeiros n inteiros positivos a qualquer poder. Para calcular a soma dos primeiros n inteiros positivos elevados à kth potência, seria necessário saber cada número Bernoulli até ao kth Bernoullinumber. Cada número Bernoulli só poderia ser calculado se os números Bernoulli anteriores fossem conhecidos. Mas calcular uma longa série de números Bernoullinumbers era significativamente mais fácil do que derivar cada fórmula de soma de potências, pelo que a descoberta de Bernoulli foi um grande avanço para a matemática.
Babbage
Charles Babbage nasceu em 1791, quase um século após a morte de Bernoulli. Tive sempre uma vaga ideia de que Babbage desenhou mas não construiu um computador mecânico. Mas nunca compreendi inteiramente como é que esse computador era suposto funcionar a reboque. As ideias básicas, como acontece, não são assim tão difíceis de apreender, o que é uma boa notícia. O programa de Lovelace foi concebido para funcionar numa das máquinas de Babbage, por isso precisamos de fazer outro desvio rápido aqui para falar sobre como essas máquinas funcionavam.
Babbage concebeu duas máquinas de computação mecânica separadas. A sua primeira máquina chamava-se o Motor da Diferença. Antes da invenção da calculadora de bolso, as pessoas baseavam-se em tabelas logarítmicas para calcular os números de grandes quantidades do produto. (Há um bom Numerophilevideo sobre como isto era feito.) As grandes tabelas logarítmicas não são difíceis de criar, pelo menos conceptualmente, mas o simples número de cálculos que precisam de ser feitos para os criar significava que no tempo deBabbage continham frequentemente erros. Babbage, frustrado com isto, procurou criar uma máquina que pudesse tabular logaritmos mecanicamente e, portanto, sem erros.7
O Difference Engine não era um computador, porque tudo o que fazia era adicionar e subtrair. Aproveitou um método concebido pelo matemático francês Gaspard de Prony que quebrou o processo de tabulação dos logaritmos em passos pequenos.8 Estes pequenos passos envolviam apenas adição e subtracção,o que significava que um pequeno exército de pessoas sem qualquer treino especial de aptidão matemática poderia ser utilizado para produzir uma tabela. O método de De Prony, conhecido pelo método das diferenças divididas, poderia ser usado para tabular qualquer polinómio. Os polinómios, por sua vez, poderiam ser usados para aproximar funções logarítmicas e trigonométricas.
Para ter uma noção de como este processo funcionava, considere a seguinte função polinomial simples:
\p> O método das diferenças divididas implica encontrar a diferença entre o valor eachsuccessivo de y para valores diferentes de x. As diferenças entre estas diferenças são então encontradas, e possivelmente as diferenças entre as próprias diferenças seguintes, até aparecer uma diferença constante. Estas diferenças podem então ser utilizadas para obter o próximo valor do polinómio simplesmente por aditamento.
Porque o polinómio acima é apenas um polinómio de segundo grau, somos capazes de detectar a diferença constante após apenas duas colunas de diferenças:
| x | y | Diff 2 | |
|---|---|---|---|
| 1 | 2 | ||
| 2 | 5 | 3 | |
| 10 | 5 | 2 | |
| 4 | 17 | 7 | 2 |
| 5 | ? | ? | 2 |
| … | … | … | … |
Agora, uma vez que sabemos que a diferença constante é 2, podemos encontrar o valor de quando x é 5 apenas através da adição. Se adicionarmos 2 a 7, a última entrada na coluna “Diff 1”, obtemos 9. Se adicionarmos 9 a 17, a última entrada na coluna “Diff 1”, obtemos 26, a nossa resposta.
Babbage’s Difference Engine tinha, para cada coluna de diferença numa tabela como a anterior, uma coluna física de engrenagens. Cada engrenagem era um dígito decimal e a coluna de toda a coluna era um número decimal. O Motor de Diferença tinha oito colunas de engrenagens, pelo que podia tabular um polinómio até ao sétimo grau. O columnswere inicialmente fixado com valores que correspondiam a uma linha inicial na tabela de diferenças, funcionava antes do tempo. Um operador humano virava então um eixo de manivela,fazendo com que a diferença constante se propagasse através da máquina, uma vez que o valor armazenado em cada coluna era adicionado ao seguinte.
Babbage era capaz de construir uma pequena secção do Motor de Diferença e usá-lo para demonstrar as suas ideias em festas.9 Mas mesmo depois de gastar uma quantia de dinheiro público igual ao custo de dois grandes navios de guerra, nunca construiu a máquina inteira.10 Babbage não conseguiu encontrar ninguém no início do século XIX que pudesse fazer o número de engrenagens de que necessitava com precisão suficiente. Uma DifferenceEngine funcional só seria construída nos anos 90, após o advento da maquinaria de precisão. Há um grande vídeo no YouTube demonstrando um Motor de Diferença funcional emprestado ao Museu de História da Informática em Mountain View, que vale a pena assistir mesmo só para ouvir os maravilhosos sons que a máquina faz enquanto funciona.
Babbage acabou por perder o interesse no Motor de Diferença quando percebeu que poderia ser construída uma máquina muito mais potente e flexível. O seu Engenho Analítico era a máquina que conhecemos hoje como o computador mecânico de Babbage. O Motor Analítico baseava-se nas mesmas colunas de engrenagens utilizadas no DifferenceEngine, mas enquanto o Difference Engine só tinha oito colunas, o Motor Analítico deveria ter muitas mais centenas. O AnalyticalEngine podia ser programado usando cartões perfurados como um Tear Jacquard e podia multiplicar e dividir, bem como adicionar e subtrair. Para realizar uma destas operações, uma secção da máquina chamada “moinho” reordenar-se-ia na configuração apropriada, leria os operandos de outras colunas utilizadas para o armazenamento de dados, e depois escreveria o resultado de volta para outra coluna.
Babbage chamou à sua nova máquina o Motor Analítico porque era potente o suficiente para fazer algo parecido com análise matemática. O Motor Analítico poderia tabular um polinómio, mas o Motor Analítico seria capaz de calcular, por exemplo, os coeficientes da expansão do polinómio de outra expressão. Era uma máquina espantosa, mas o governo britânico decidiu-se a financiar a sua construção. Assim, Babbage foi para o estrangeiro a Itália para tentar apoiar a sua ideia.
Notas do Tradutor
Em Turim, Babbage encontrou-se com o engenheiro italiano e futuro primeiro-ministro LuigiMenabrea. Ele persuadiu Menabrea a escrever um esboço do que a AnalyticalEngine poderia realizar. Em 1842, Menabrea publicou um artigo sobre o tema em francês. No ano seguinte, Lovelace publicou uma tradução de Menabrea’spaper para inglês.
Lovelace, então conhecida como Ada Byron, conheceu Babbage numa festa em 1833, quando tinha 17 anos e 41.11 Lovelace ficou fascinado com Babbage’sDifference Engine. Ela também podia compreender como funcionava, porque tinha sido amplamente instruída em matemática durante toda a sua infância. A sua mãe, Annabella Milbanke, tinha decidido que uma base sólida em matemática iria desviar a sensibilidade selvagem e romântica que possuía o pai de Lovelace, Lord Byron, o famoso poeta. Depois de se encontrarem em 1833, Lovelace e Babbage permaneceram separados do mesmo círculo social e escreveram um ao outro frequentemente.
Ada Byron casou com William King em 1835. King tornou-se mais tarde Conde de Lovelace, fazendo de Ada a Condessa de Lovelace. Mesmo depois de ter tido três filhos, ela continuou a sua educação em matemática, empregando Augustus de Morgan, que descobriu as leis de De Morgan, como seu tutor.12 Lovelace viu imediatamente o potencial da Máquina Analítica de Lovelace e estava ansiosa por trabalhar com ele para promover a ideia. Uma amiga sugeriu que ela traduzisse o trabalho de Menabrea para uma audiência inglesa.13
O trabalho de Menabrea deu uma breve visão geral de como o Motor Analítico funcionava,depois mostrou como o Motor Analítico seria uma máquina muito superior. O Motor Analítico seria tão potente que poderia “formar o produto de dois números, cada um contendo vinte figuras, em três minutos “14 (ênfase no original). Menabrea deu mais exemplos das capacidades da máquina, demonstrando como poderia resolver um sistema simples de equações lineares e expandir o produto de duas expressões binomiais. Em ambos os casos, Menabreaprovou o que Lovelace chamou de “diagramas de desenvolvimento”, que listavam esta sequência de operações que teriam de ser realizadas para calcular a resposta correcta.15 Estes eram programas no mesmo sentido que o próprio programa de Lovelace era um programa e foram originalmente publicados no ano anterior. Mas como veremos, os programas de Menabrea eram apenas simples exemplos do que era possível.Todos eles eram triviais no sentido em que não exigiam qualquer tipo de ramificação ou looping.
Lovelace anexou uma série de notas à sua tradução do trabalho de Menabrea que, no seu conjunto, funcionou muito mais tempo do que o trabalho original. Foi aqui que ela deu as suas maiores contribuições para a informática. Na Nota A, que Lovelace anexou à descrição inicial do Motor Analítico de Menabrea, Lovelace explicou com grande comprimento e muitas vezes em linguagem lírica a promessa de uma máquina que poderia executar operações matemáticas arbitrárias. Ela previu que uma máquina como o Motor Analítico não se limitava apenas aos números e podia de facto actuar sobre quaisquer objectos “cujas relações fundamentais mútuas poderiam ser expressas por aqueles da ciência abstracta das operações, e que também deveriam ser susceptíveis de adaptações à acção da notação de operação e do mecanismo do motor “16 , acrescentou que a máquina poderia um dia, por exemplo, composemúsica. Esta percepção foi tanto mais notável quanto Menabrea viu o Motor Analítico principalmente como uma ferramenta para automatizar “a computação longa e árida”, o que libertaria as capacidades intelectuais dos cientistas brilhantes para um pensamento mais avançado.17 A previsão milagrosa que Lovelace demonstrou na Nota A é uma das principais razões pelas quais ela é celebrada hoje.
A outra nota famosa é a Nota G. Lovelace começa a nota G argumentando que, apesar dos seus impressionantes poderes, a Máquina Analítica não pode realmente ser dita para “pensar”. Esta parte da Nota G é aquilo a que Alan Turing se referiria mais tarde como “Objecção de LadyLovelace”. No entanto, Lovelace continua, a máquina pode fazer coisas extraordinárias. Para ilustrar a sua capacidade de lidar com problemas ainda mais complexos, Lovelace fornece o seu programa calculando os números Bernoulli.
O programa completo, no formato expandido de “diagrama de desenvolvimento” que Lovelace explica na Nota D, pode ser seenhere.O programa é essencialmente uma lista de operações, especificadas usando os símbolos matemáticos de uso. Não parece que Babbage ou Lovelace tenha chegado tão longe no desenvolvimento de algo como um conjunto de códigos op para o Motor Analítico.
Embora Lovelace estivesse a descrever um método para calcular toda a sequência de números de Bernoulli até algum limite, o programa que ela forneceu apenas ilustrou uma etapa desse processo. O seu programa calculou um número que ela chamou B7, que os matemáticos modernos conhecem como o oitavo número de Bernoulli. O seu programa procurou resolver a seguinte equação:
\\p>p>Na equação acima, cada termo representa um coeficiente na fórmula polinomial para a soma dos números inteiros a um determinado poder. Aqui esse poder é oito, uma vez que o oitavo número de Bernoulli aparece pela primeira vez na fórmula para a soma dos inteiros positivos à oitava potência. Os números B e A representam os dois tipos de offactores que Bernoulli descobriu. B1 até B7 são todos diferentes números Bernoullinumbers, indexados de acordo com a indexação de Lovelace. A0 até A5 representam os factores dos coeficientes que Bernoulli pôde calcular utilizando o triângulo de Pascal. Os valores de A0, A1, A3, e A5 aparecem abaixo. Aqui n representa o índice do número Bernoulli na sequência de números ímpares de Bernoullinumbers, começando com o primeiro. O programa de Lovelace utilizado n = 4,\\p>criei atranslação do programa de Lovelace para C, o que pode ser mais fácil de seguir. O programa de Lovelace calcula primeiro A0 e o produto B1A1. Em seguida, entra num laço que repete duas vezes para calcular B3A3 e B5A5, uma vez que estes são formados de acordo com um padrão idêntico. Depois de cada produto ser calculado, é adicionado com todos os produtos anteriores, de modo que no final do programa a soma total tenha sido obtida.
Obviamente a tradução C não é uma recriação exacta do programa de Lovelace. Declara variáveis na pilha, por exemplo, enquanto as variáveis de Lovelace eram mais parecidas com registos. Mas torna óbvias as partes do programa de Lovelace que eram tão prescientes. O programa C contém dois while loops, um aninhado dentro do outro. O programa de Lovelace não tinha while loops exactamente, mas fazia grupos de operações e no texto da sua nota especificava quando deveriam repetir-se. A variável v10, no programa original e na Ctradução, funciona como uma contra-variável que decreta com cada laço, aconselhando qualquer programador a estar familiarizado com o mesmo. De facto, para além da multiplicação de variáveis com nomes inúteis, a tradução em C do programa de Lovelace não parece nada alienígena.
A outra coisa que vale a pena mencionar rapidamente é que a tradução do programa de Lovelace para C não foi assim tão difícil, graças ao detalhe presente no seu diagrama. Ao contrário das tabelas de Menabrea, a sua tabela inclui uma coluna intitulada “Indicação de mudança no valor em qualquer variável”, o que torna muito mais fácil seguir a tradução de estado ao longo de todo o programa. Ela adiciona aqui um índice sobrescrito de cada variável para indicar os valores sucessivos que possuem. Um sobrescrito de dois, por exemplo, significa que o valor aqui utilizado é o segundo valor que foi atribuído à variável desde o início do programa.
O Primeiro Programador?
Depois de ter traduzido o programa de Lovelace para C, consegui executá-lo no meu próprio computador. Para minha frustração, continuei a obter o resultado errado. Depois de uma certa depuração, percebi finalmente que o problema não era o código que eu tinha escrito. O bug estava no original!
No seu “diagrama de desenvolvimento”, Lovelace dá a quarta operação comov5 / v4. Mas a ordem correcta aqui é v4 / v5. Isto pode muito bem ter sido um erro de tipografia e não um erro no programa que Lovelace concebeu. Mesmo assim, este deve ser o erro mais antigo em computação. Fiquei maravilhado por, durante cerca de dez minutos, sem saber, ter lutado com este primeiro bug.
Jim Randall, outro blogger que traduziu o programa de Lovelace para Python, ter notado este bug de divisão e dois outros problemas. O que é que diz sobre Ada Lovelaceth que o seu programa publicado contém bugs menores? Talvez mostre que ela estava a tentar escrever não apenas uma demonstração, mas um programa real. Afinal de contas, poderá realmente estar a escrever algo mais do que programas de brinquedos se não estiver também a escrever muitos bugs?
Um artigo da Wikipedia chama Lovelace o primeiro a publicar um “complexprograma “18 Talvez seja a forma correcta de pensar sobre a realização de Lovelace. Menabrea publicou “diagramas de desenvolvimento” no seu artigo um ano antes de Lovelace ter publicado a sua tradução. Babbage também escreveu mais de vinte programas que nunca publicou.19 Por isso, não é muito correcto dizer que Lovelace escreveu ou publicou o primeiro programa, embora haja sempre espaço para questionar sobre o que constitui exactamente um “programa”. Mesmo assim, o programa de Lovelace estava quilómetros à frente de qualquer outro que já tivesse sido publicado anteriormente. O programa mais longo que Menabrea apresentou foi 11 operações de longa duração e continha noloops ou ramos; o programa de Lovelace contém 25 operações e um ciclo aninhado (e assim ramificando). Menabrea escreveu o seguinte no final do seu trabalho:
Quando o motor tiver sido construído, a dificuldade será reduzida à elaboração das cartas; mas como estas são meramente a tradução de fórmulas algébricas, será, através de alguma notação simples, fácil atribuir a execução das mesmas a um operário.20
Nem Babbage nem Menabrea estavam especialmente interessados em aplicar o Motor Analítico a problemas para além dos desafios matemáticos imediatos que levaram primeiro Babbage a construir máquinas de cálculo. Lovelace viu que o Motor Analítico era capaz de muito mais do que Babbage ou Menabrea podiaimagine. Lovelace também compreendeu que “a fabricação das cartas” não seria mera ideia posterior e que poderia ser bem ou mal feita. Isto é difícil de apreciar sem compreender o seu programa a partir da Nota G e ver por si próprio o cuidado que pôs na sua concepção. Mas depois de o ter feito, pode dizer-se que Lovelace, mesmo que ela não tenha sido a primeira programadora, foi a primeira programadora a merecer o título.
Se gostou deste post, mais como se saísse a cada quatro semanas! Siga @TwoBitHistory no Twitter ou subscreva o feed RSS para se certificar de que sabe quando um novo post é publicado.
Anteriormente em TwoBitHistory…
O post desta semana: O prestigioso pedigree de Parsing Vim!https://t.co/1YUszI5dIC
– TwoBitHistory (@TwoBitHistory) 5 de Agosto de 2018
-
Walter Isaacson, The Innovators (Nova Iorque: Simon & Schuster Paperbacks, 2015), 25.
-
Janet Beery, “Sums of Powers of Positive Integers” (Sums of Powers of Positive Integers): Archimedes,” Mathematical Association of America, acedido a 18 de Agosto de 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-archimedes-287-212-bce-greece-italy.
-
Janet Beery, “Sums of Powers of Positive Integers”: Abu Ali Al-Hasan Ibn Al-Hasan Ibn Al-Haytham,” Mathematical Association of America, acedido a 18 de Agosto de 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-abu-ali-al-hasan-ibn-al-hasan-ibn-al-haytham-965-1039-egypt.
-
Janet Beery, “Sums of Powers of Positive Integers”: Conclusão,” Mathematical Association of America, acedido a 18 de Agosto de 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-conclusion.
-
Janet Beery, “Sums of Powers of Positive Integers”: Blaise Pascal,” Mathematical Association of America, acedido a 18 de Agosto de 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-blaise-pascal-1623-1662-france.
- p>Janet Beery, “Sums of Powers of Positive Integers”: Jakob Bernoulli,” Mathematical Association of America, acedido a 18 de Agosto de 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-jakob-bernoulli-1654-1705-switzerland.
-
Isaacson, 19.
-
Isaacson, 20.
-
Robert Scoble, “A Demo of Charles Babbage’s Difference Engine”, YouTube, 17 de Junho de 2010, acedido a 18 de Agosto de 2018, https://www.youtube.com/watch?v=BlbQsKpq3Ak&feature=youtu.be&t=7m37s.
-
Isaacson, 22.
-
Isaacson, 8.
-
Isaacson, 17.
-
Isaacson, 25.
-
Luigi Menabrea, “Sketch of the Analytical Engine”, Scientific Memoirs 3 (1843): 686, acedido a 18 de Agosto de 2018, https://books.google.com/books/about/Scientific_Memoirs_Selected_from_the_Tra.html?id=qsY-AAAAYAAJ.
-
Ada Lovelace, “Translator’s Notes to M. Menabrea’s Memoir,” Scientific Memoirs 3 (1843): 712, acedido a 18 de Agosto de 2018, https://books.google.com/books/about/Scientific_Memoirs_Selected_from_the_Tra.html?id=qsY-AAAAYAAJ.
-
Lovelace, 694.
-
Menabrea, 690.
-
“Número Bernoulli”, Wikipedia, acedido a 18 de Agosto de 2018, https://en.wikipedia.org/wiki/Bernoulli_number.
-
Isaacson, 29.
-
Menabrea, 689.