Sabemos calcular la expresión 5 x 5. Esta expresión se puede escribir de forma más corta utilizando algo llamado exponentes.
$5\cdot 5=5^{2}$
Una expresión que representa la multiplicación repetida de un mismo factor se llama potencia.
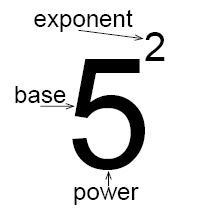
El número 5 se llama base, y el número 2 se llama exponente. El exponente corresponde al número de veces que la base se utiliza como factor.
| 31 | 3 a la primera potencia | 3 |
| 4 a la segunda potencia o 4 al cuadrado | 4 ∙ 4 | 53 | 5 a la tercera potencia o 5 al cubo | 5 ∙ 5 ∙ 5 | 26 | 2 a la potencia de seis | 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 |
Ejemplo
Escribe estas multiplicaciones como exponentes
$5\cdot 5\cdot 5=5^{3}$
$4\cdot 4\cdot 4\cdot 4=4^{5}$
$3\cdot 3\cdot 3=3^{4}$
Multiplicación
Si dos potencias tienen la misma base entonces podemos multiplicar las potencias. Cuando multiplicamos dos potencias sumamos sus exponentes.
La regla:
$x^{a}\cdot x^{b}=x^{a+b}$
Ejemplo
$4^{2}\cdot 4^{5}=left ( 4\cdot 4 \right )\cdot \left ( 4\cdot 4\cdot 4\cdot 4\cdot 4 \ right )=4^{7}=4^{2+5}$
División
Si dos potencias tienen la misma base entonces podemos dividir las potencias. Cuando dividimos potencias restamos sus exponentes.
La regla:
$\frac{x^{a}}{ x^{b}}=x^{a-b}$
Ejemplo
$frac{4^{2}}{ 4^{5}}={frac{color{rojo}{no}{4}{cdot{color{rojo}} {{no}{4}} {{color}{rojo}{no}{4}}=4^{-3}=4^{2-5}$
Un exponente negativo es igual al recíproco del exponente positivo.
$x^{-a}=\frac{1}{x^{a}}$
Ejemplo
$2^{-3}=\frac{1}{2^{3}}$
Cuando se eleva un producto a una potencia se eleva cada factor con una potencia
$(x\cdot y)^{a}=x^{a}\cdot y^{a}$
Ejemplo
$(2x)^{4}=2^{4}\cdot x^{4}=16x^{4}$
La regla de la potencia de una potencia y la potencia de un producto se pueden combinar en la siguiente regla:
$(x^{a}\cdot y^{b})^{z}=x^{a\cdot z}\cdot y^{b\cdot z}$
Ejemplo
$(x^{3}\cdot y^{4})^{2}=x^{3\cdot 2}\cdot y^{4\cdot 2}=x^{6}\cdot y^{8}$
Video lecciones
Redactar las expresiones
$2\cdot 2\cdot 2$
$x\cdot x\cdot x\cdot x$