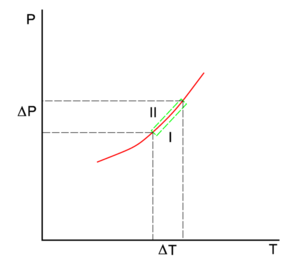
La línea roja del diagrama P-T es la curva de coexistencia de dos fases, I y II, de un sistema monocomponente. La fase I puede ser el vapor y la II la fase líquida del componente. La línea verde inferior da la pendiente en la fase I y la línea verde superior en la fase II.
La relación Clausius-Clapeyron es una ecuación para un sistema monocomponenteconsistente en dos fases en equilibrio termodinámico a temperatura absoluta constante T y presión constante P. Una curva en un diagrama termodinámico bidimensional que separa dos fases en equilibrio se conoce como curva de coexistencia. La relación Clausius-Clapeyron da la pendiente de la curva de coexistencia en el diagrama P-T:
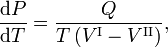
donde Q es el calor molar de transición. Es el calor necesario para llevar un mol del compuesto que constituye el sistema de la fase II a la fase I; también se conoce como calor latente. Para las transiciones de fase con P constante, es la entalpía de transición molar. Por ejemplo, cuando la fase II es un líquido y la fase I es un vapor, entonces Q ≡ Hv es el calor molar de vaporización (también conocido como entalpía molar de evaporación). Además, V I es el volumen molar de la fase I a la presión P y a la temperatura T del punto en el que se considera la pendiente y V II es lo mismo para la fase II.
La ecuación lleva el nombre de Émile Clapeyron, que la publicó en 1834, y de Rudolf Clausius, que la puso sobre una base termodinámica firme en 1850.
Contenidos
- 1 Derivación
- 2 Solución aproximada
- 3 Aplicación
- 4 Referencia
- El volumen molar de la fase II es despreciable comparado con el volumen molar de la fase I: V I >> V II. En general, lejos del punto crítico, esta desigualdad se mantiene bien para los equilibrios líquido-gas.
- La fase I satisface la ley de los gases ideales, donde R es la constante molar de los gases,
- El calor de transición (latente) Q es constante en el intervalo de integración de la temperatura. Las integraciones van de la temperatura inferior T1 a la superior T2 y de P1 a P2.
Derivación
La condición de la termodinámica es el resultado de una serie de factores.
La condición de equilibrio termodinámico a presión constante P y temperatura constante T entre dos fases I y II es la igualdad de las energías libres molares de Gibbs G,
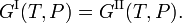
La energía libre de Gibbs molar de la fase α (α = I, II) es igual al potencial químicoμα de esta fase. Por tanto, la condición de equilibrio puede escribirse como,
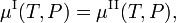
que se cumple en todas partes a lo largo de la curva de coexistencia (roja) de la figura.
Si vamos reversiblemente a lo largo de la línea verde inferior y superior de la figura , los potenciales químicos de las fases, siendo funciones de T y P, cambian en ΔμI y ΔμII, para la fase I y II, respectivamente, mientras el sistema permanece en equilibrio,
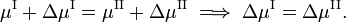
Desde la termodinámica clásica se sabe que
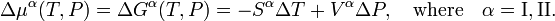
Aquí Sα es la entropía molar (entropía por mol) de la faseα y Vα es el volumen molar (volumen de un mol) de estafase. Se deduce que
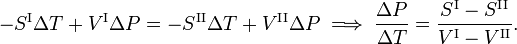
De la segunda ley de la termodinámica se sabe que para una transición de fase reversible se cumple que
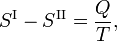
donde Q es la cantidad de calor necesaria para convertir un mol decompuesto de la fase II en la fase I. Eliminando la entropía y tomando el límite de cambios infinitesimales en T y P se obtiene la ecuación de Clausius-Clapeyr,
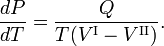
Solución aproximada
La ecuación de Clausius-Clapeyron es exacta. Cuando se hacen las siguientes suposiciones, se puede integrar:
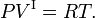Si la fase I es un gas y la presión es bastante baja, esta suposición es razonable.
Bajo esta condición la ecuación de Clausius-Clapeyron se convierte en
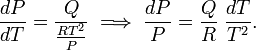
La integración da
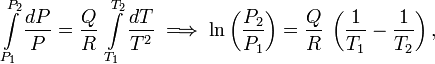
Aplicación
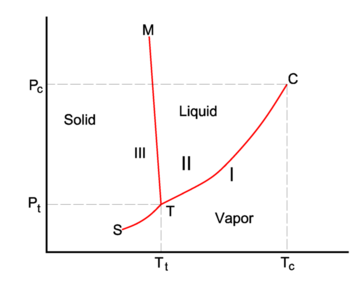
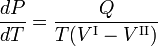
dice la pendiente de las tres curvas de coexistencia (equilibrio, rojo). La línea de ebullición T-C tiene una pendiente positiva, porque el calor de vaporización Q = Hv es positivo y el volumen molar del vapor V I es (mucho) mayor que el del líquido V II. Por una razón similar, la línea de sublimación (transición de sólido a vapor) T-S tiene una pendiente positiva. La línea de sublimación T-S es más empinada que la línea de ebullición T-C porque el calor de sublimación es mayor que el calor de vaporización, mientras que en la vecindad del punto de cruce T (el punto triple) la diferencia de volúmenes molares es casi igual. La línea de fusión T-M tiene una pendiente negativa, lo que ocurre sólo para unos pocos compuestos (entre ellos el agua). Consideremos
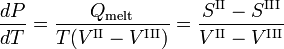
El volumen molar VIII del sólido es mayor que el volumen molar VII del líquido, mientras que la entalpía de fusión Qmelt = SII-SIII > 0 (un líquido tiene una entropía mayor que el sólido correspondiente, cuesta energía fundir un sólido). Los compuestos que tienen líneas de fusión con pendiente negativa, tienen una fase sólida de menor densidad que la fase líquida. Por ejemplo, es muy conocido que el agua sólida (hielo) flota sobre el agua líquida.
El punto C es el punto crítico. Más allá de este punto el vapor y el líquido son un solo fluido indistinguible. No hay transición de fase o una interfaz de fase a la derecha de la línea de fusión y por encima de la línea de constante P = Pc. El fluido gas/líquido también aparece a la derecha de la línea de constante T = Tc.
La relación Clausius-Clapeyron también es válida para las transiciones entre diferentes fases cristalinas.