Una prueba t independiente de dos muestras puede ejecutarse sobre los datos de la muestra de una variable numérica de resultado distribuida normalmente para determinar si su media difiere entre dos grupos independientes. Por ejemplo, podríamos ver si la media de la GPA difiere entre los estudiantes universitarios de primer y último año recogiendo una muestra de cada grupo de estudiantes y registrando sus GPAs.
Hipótesis:
Ho: La media poblacional de un grupo es igual a la media poblacional del otro grupo, o μ1 = μ2
HA: La media poblacional de un grupo no es igual a la media poblacional del otro grupo, o μ1 ≠ μ2
Esta prueba también puede realizarse con una hipótesis alternativa direccional:
Ho: La media poblacional de un grupo es igual a la media poblacional del otro grupo, o μ1 = μ2
Ha: La media poblacional de un grupo es mayor que la media poblacional del otro grupo, o μ1 > μ2
La estadística de la prueba para una prueba t independiente de dos muestras se calcula tomando la diferencia de las dos medias muestrales y dividiéndola por el error estándar estimado agrupado o no agrupado. El error estándar estimado es una medida agregada de la cantidad de variación en ambos grupos.
Ecuaciones relevantes:
Grados de libertad: Varía según las condiciones, pero la regla básica para los cálculos manuales es el menor de n1 – 1 y n2 – 1, donde n es el tamaño de la muestra para cada grupo.
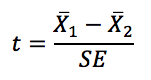
Supuestos:
- Muestras aleatorias
- Observaciones independientes
- La población de cada grupo se distribuye normalmente.
- Las varianzas de la población son iguales.
Si no se cumple el tercer supuesto, la prueba alternativa es la prueba U de Mann-Whitney, que puede ejecutarse para ver si hay una diferencia entre dos grupos para una variable con cualquier tipo de distribución.
Si se cumple el cuarto supuesto, entonces se utiliza el error estándar estimado agrupado en el cálculo de la estadística de la prueba. Si el cuarto supuesto no se cumple, entonces se utiliza el error estándar estimado no agrupado, que es más conservador (y la prueba se denomina «Prueba de Welch»).
Ejemplo 1: Vídeo de cálculo manual
Este ejemplo analiza el número medio de horas dormidas de los estudiantes masculinos frente a los femeninos.


Conclusión de la muestra: Con t(df=40)=1,73, que fue más extremo que nuestro valor crítico de 1,68, estos datos sí proporcionan evidencia de que las estudiantes sí duermen más, en promedio, que los estudiantes varones.
Ejemplo 2: Cómo ejecutar en Excel 2016
Algunos de estos análisis requieren que tenga habilitado el complemento Data Analysis ToolPak en Excel. Para obtener instrucciones sobre cómo realizar este análisis en versiones anteriores de Excel, visite https://stat.utexas.edu/videos
En este tutorial, determinará si los hombres y las mujeres difieren en su nivel de felicidad.
NOTA: En este vídeo, la prueba t se realiza asumiendo varianzas desiguales (Prueba de Welch).
Conjunto de datos utilizado en el vídeo
Direcciones del PDF correspondiente al vídeo
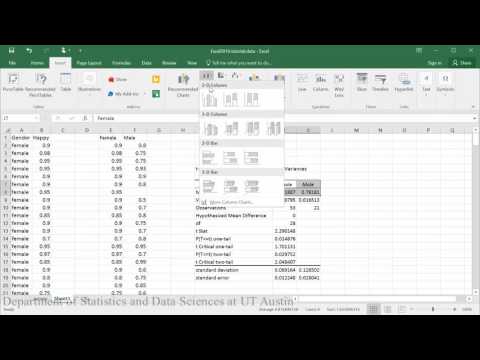

Conclusión de la muestra: Con t(df=28)=2,29, p<0,05, estos datos sí proporcionan evidencia de que las estudiantes son más felices, en promedio, que los estudiantes varones.
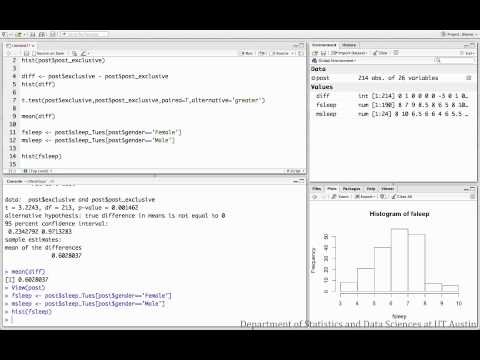
Ejemplo 3: Cómo ejecutar en RStudio
Este ejemplo analiza el número medio de horas dormidas para los estudiantes varones frente a las mujeres.
NOTA: En este vídeo, la prueba t se realiza asumiendo varianzas desiguales (Prueba de Welch).
Conjunto de datos utilizado en el vídeo
Archivo de script R utilizado en el vídeo