 |
Proprio come le trasformazioni in geometria, possiamo spostare e ridimensionare i grafici delle funzioni |
Cominciamo con una funzione, in questo caso è f(x) = x2, ma potrebbe essere qualsiasi cosa:
f(x) = x2
Ecco alcune semplici cose che possiamo fare per spostarla o scalarla sul grafico:
Possiamo spostarla in alto o in basso aggiungendo una costante al valore y:
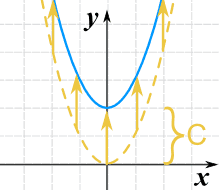
g(x) = x2 + C
Nota: per spostare la linea in basso, usiamo un valore negativo per C.
- C > 0 la sposta in alto
- C < 0 la sposta in basso
Possiamo spostarla a sinistra o a destra aggiungendo una costante al valore di x:
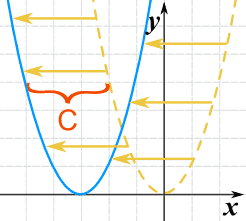
g(x) = (x+C)2
Aggiungendo C si sposta la funzione a sinistra (la direzione negativa).
Perché? Beh, immaginate di ereditare una fortuna quando la vostra età = 25 anni. Se lo cambiate in (età+4) = 25 allora la riceverete a 21 anni. L’aggiunta di 4 lo fa accadere prima.
- C > 0 lo sposta a sinistra
- C < 0 lo sposta a destra
Ma dobbiamo aggiungere C ovunque appaia x nella funzione (stiamo sostituendo x+C a x).
Esempio: la funzione v(x) = x3 – x2 + 4x
Per spostare C spazi a sinistra, aggiungere C a x ovunque appaia x:
w(x) = (x + C)3 – (x + C)2 + 4(x + C)
Un modo semplice per ricordare cosa succede al grafico quando si aggiunge una costante:
aggiungere a y per andare in alto
aggiungere a x per andare a sinistra
Possiamo allungare o comprimere in direzione y moltiplicando l’intera funzione per una costante.
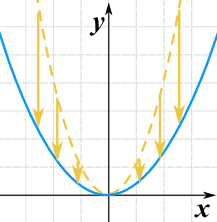
g(x) = 0.35(x2)
- C > 1 lo allunga
- 0 < C < 1 lo comprime
Si può allungare o comprimere in direzione x-moltiplicando x per una costante.
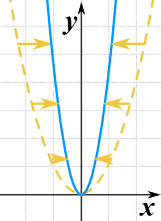
g(x) = (2x)2
- C > 1 lo comprime
- 0 < C < 1 lo allunga
Nota che (a differenza della direzione y-direzione), valori più grandi causano una maggiore compressione.
Possiamo capovolgerla moltiplicando l’intera funzione per -1:
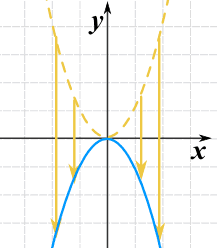
g(x) = -(x2)
Questo si chiama anche riflessione sull’asse x (l’asse dove y=0)
Possiamo combinare un valore negativo con una scalatura:
Esempio: moltiplicando per -2 si capovolge e si allunga in direzione y.
Possiamo capovolgerlo a sinistra e a destra moltiplicando il valore x per -1:
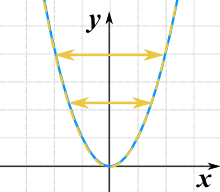
g(x) = (-x)2
Lo capovolge davvero a destra e a sinistra! Ma non puoi vederlo, perché x2 è simmetrico rispetto all’asse y. Quindi ecco un altro esempio usando √(x):
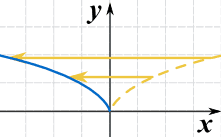
g(x) = √(-x)
Questo si chiama anche riflessione sull’asse y(l’asse dove x=0)
Sommario
| y = f(x) + C |
|
| y = f(x + C) |
|
| y = Cf(x) |
|
| y = f(Cx) |
|
| y = -f(x) |
|
| y = f(-x) |
|
Esempi
Esempio: la funzione g(x) = 1/x
Ecco alcune cose che possiamo fare:
Esempio: la funzione v(x) = x3 – 4x
Ecco alcune cose che possiamo fare:
= 2×3 – 8x
= 27×3 – 12x
Tutto in uno ….
Possiamo fare tutte le trasformazioni in una volta sola usando questo:
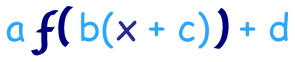
a è l’allungamento/compressione verticale
- |a| > 1 allunga
- |a| < 1 comprime
- a < 0 capovolge il grafico in giù
b è tratto/compressione orizzontale
- |b| > 1 comprime
- |b| < 1 allunga
- b < 0 capovolge il grafico da sinistra adestra
c è lo spostamento orizzontale
- c < 0 si sposta a destra
- c > 0 si sposta a sinistra
d è lo spostamento verticale
- d > 0 si sposta verso l’alto
- d < 0 si sposta verso il basso
