Volver al índice de lecciones | Hacer las lecciones en orden | Página para imprimir
Funciones exponenciales: Interés compuesto (página 4 de 5)
Secciones: Introducción, Evaluación, Graficación, Interés compuesto, La exponencial natural
Una ecuación exponencial muy importante es la fórmula del interés compuesto:
- Suponga que planea necesitar 10.000 dólares dentro de treinta y seis meses cuando su hijo empiece a ir a la universidad. Quiere invertir en un instrumento que rinda un 3,5% de interés, compuesto mensualmente. ¿Cuánto debería invertir?
![]()
…donde «A» es el importe final, «P» es el importe inicial (o «principal»), «r» es el tipo de interés (expresado en forma de decimal), «n» es el número de capitalizaciones al año y «t» es el número total de años.
Respecto a las variables, n se refiere al número de capitalizaciones en un año cualquiera, no al número total de capitalizaciones durante la vida de la inversión. Si el interés se compone anualmente, entonces n = 1; si es semestral, entonces n = 2; trimestral, entonces n = 4; mensual, entonces n = 12; semanal, entonces n = 52; diario, entonces n = 365; y así sucesivamente, independientemente del número de años. Además, «t» debe expresarse en años, porque los tipos de interés se expresan así. Si un ejercicio indica que el capital se invirtió durante seis meses, habría que convertirlo en 6/12 = 0,5 años; si se invirtió durante 15 meses, entonces t = 15/12 = 1,25 años; si se invirtió durante 90 días, entonces t = 90/365 de un año; y así sucesivamente.
Nótese que, para cualquier tipo de interés dado, la fórmula anterior se simplifica a la forma exponencial simple a la que estamos acostumbrados. Por ejemplo, dejemos que el tipo de interés r sea del 3%, compuesto mensualmente, y que el importe de la inversión inicial sea de 1250 dólares. Entonces la ecuación de interés compuesto, para un periodo de inversión de t años, se convierte en:
![]()
…donde la base es 1.0025 y el exponente es la expresión lineal 12t.
Para hacer problemas de palabras de interés compuesto, generalmente la única parte difícil es averiguar qué valores van donde en la fórmula de interés compuesto. Una vez que tengas todos los valores enchufados correctamente, puedes resolver para cualquier variable que quede.
Publicidad
Para resolver esto, tengo que averiguar qué valores van con qué variables. En este caso, quiero acabar con 10.000 dólares, por lo que A = 10.000. El tipo de interés es del 3,5%, por lo que, expresado como decimal, r = 0,035. El plazo es de treinta y seis meses, por lo que t = 36/12 = 3. Y el interés se compone mensualmente, por lo que n = 12. La única variable que queda es P, que representa la cantidad con la que empecé. Dado que estoy tratando de averiguar cuánto invertir en primer lugar, resolver para P tiene sentido. Voy a introducir todos los valores conocidos y luego resolveré la variable restante:
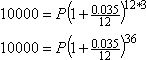
La tentación en este punto es simplificar en el lado derecho, y luego dividir para resolver para P. No hagas eso; tiende a un error de redondeo, y puede meterte en problemas más adelante. En su lugar, mantente exacto y haz primero la división simbólica (y exacta):
![]()
Ahora haré toda la simplificación en mi calculadora, trabajando desde dentro hacia fuera, para que todo se lleve en la memoria y obtenga una respuesta lo más exacta posible:

Necesito invertir unos 9004 dólares.62.
(El problema no especificaba cómo redondear, pero en este caso no hacía falta. Los problemas de dólares y centavos siempre redondean a dos decimales). Copyright © Elizabeth Stapel 2002-2011 Todos los derechos reservados
Debes memorizar la fórmula del interés compuesto, pero también debes memorizar el significado de cada una de las variables de la fórmula. Si bien es posible que te den la fórmula en el examen, es poco probable que te den los significados de las variables y, sin los significados, no podrás completar los ejercicios.
<< Anterior Arriba | 1 | 2 | 3 | 4 | 5 | Volver al índice Siguiente >>
|
Cite este artículo como: |
Stapel, Elizabeth. «Funciones exponenciales: El interés compuesto». Purplemath. Disponible en 2016
|
.