 |
Comme les transformations en géométrie, nous pouvons déplacer et redimensionner les graphes des fonctions |
Démarrons avec une fonction, dans ce cas c’est f(x) = x2, mais cela peut être n’importe quoi :
f(x) = x2
Voici quelques choses simples que nous pouvons faire pour la déplacer ou la mettre à l’échelle sur le graphique :
Nous pouvons la déplacer vers le haut ou le bas en ajoutant une constante à la valeur y :
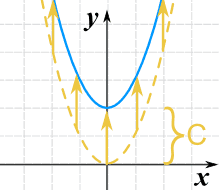
g(x) = x2 + C
Note : pour déplacer la ligne vers le bas, nous utilisons une valeur négative pour C.
- C > 0 la déplace vers le haut
- C < 0 la déplace vers le bas
Nous pouvons la déplacer à gauche ou à droite en ajoutant une constante à la valeur x :
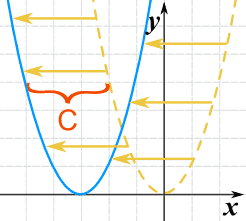
g(x) = (x+C)2
Ajouter C déplace la fonction vers la gauche (la direction négative).
Pourquoi ? Eh bien imaginez que vous allez hériter d’une fortune lorsque votre âge=25 ans. Si vous changez cela en (âge+4) = 25 alors vous l’obtiendrez quand vous aurez 21 ans. Le fait d’ajouter 4 a permis que cela se produise plus tôt.
- C > 0 le déplace vers la gauche
- C < 0 le déplace vers la droite
Mais nous devons ajouter C partout où x apparaît dans la fonction (nous substituons x+C à x).
Exemple : la fonction v(x) = x3 – x2 + 4x
Pour déplacer C espaces vers la gauche, il faut ajouter C à x partout où x apparaît :
w(x) = (x + C)3 – (x + C)2 + 4(x + C)
Une façon simple de se rappeler ce qui se passe sur le graphique quand on ajoute une constante :
ajouter à y pour aller en haut
ajouter à x pour aller à gauche
Nous pouvons l’étirer ou le comprimer dans la direction y en multipliant la fonction entière par une constante.
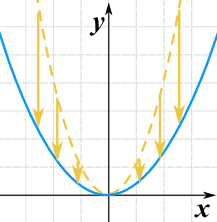
g(x) = 0.35(x2)
- C > 1 l’étire
- 0 < C < 1 le comprime
Nous pouvons l’étirer ou le comprimer dans la direction x-.en multipliant x par une constante.
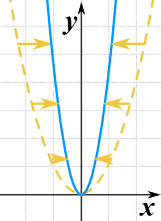
g(x) = (2x)2
- C > 1 le comprime. le
- 0 < C < 1 l’étire
Notez que (contrairement à la direction y-direction), des valeurs plus grandes entraînent une plus grande compression.
On peut la retourner en multipliant toute la fonction par -1 :
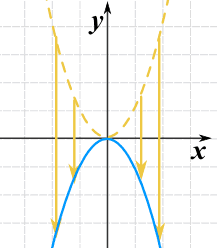
g(x) = -(x2)
C’est aussi appelé réflexion autour de l’axe x (l’axe où y=0)
On peut combiner une valeur négative avec une mise à l’échelle :
Exemple : la multiplication par -2 va la retourner ET l’étirer dans la direction des y.
On peut le retourner de gauche à droite en multipliant la valeur x par -1 :
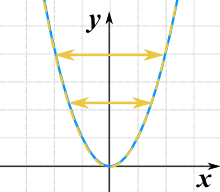
g(x) = (-x)2
Cela le retourne vraiment de gauche à droite ! Mais vous ne pouvez pas le voir, car x2 est symétrique par rapport à l’axe des y. Voici donc un autre exemple utilisant √(x) :
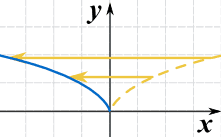
g(x) = √(-x)
Ceci est aussi appelé réflexion autour de l’axe y-.(l’axe où x=0)
Résumé
| y = f(x) + C |
|
| y = f(x + C) |
|
| y = Cf(x) |
. |
| y = f(Cx) |
|
y = -f(x) |
|
y = f(-x) |
|
Exemples
Exemple : la fonction g(x) = 1/x
Voici ce que l’on peut faire :
Exemple : la fonction v(x) = x3 – 4x
Voici ce que nous pouvons faire :
= 2×3 – 8x
= 27×3 – 12x
Tout en un …. !
Nous pouvons effectuer toutes les transformations en une seule fois en utilisant ceci :
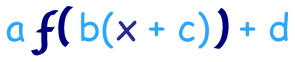
a est un étirement/compression vertical
- |a| > 1 étire
- |a| < 1 compresse
- a < 0 renverse le graphique à l’envers. vers le bas
.
b est l’étirement/la compression horizontale
- |b| > 1 compresse
- |b| < 1 étire
- b < 0 renverse le graphique de gauche à droite.droite
c est le décalage horizontal
- c < 0 décale vers la droite
- c > 0 décale vers la gauche
d est le déplacement vertical
- d > 0 se déplace vers le haut
- d < 0 se déplace vers le bas
.
