Expansiones binomiales usando el triángulo de Pascal
Considera las siguientes potencias expandidas de (a + b)n, donde a + b es un binomio cualquiera y n es un número entero. Busca patrones.
Cada expansión es un polinomio. Hay algunos patrones a tener en cuenta.
1. Hay un término más que la potencia del exponente, n. Es decir, hay términos en la expansión de (a + b)n.
2. En cada término, la suma de los exponentes es n, la potencia a la que se eleva el binomio.
3. Los exponentes de a empiezan por n, la potencia del binomio, y disminuyen hasta 0. El último término no tiene factor de a. El primer término no tiene factor de b, por lo que las potencias de b comienzan con 0 y aumentan hasta n.
4. Los coeficientes comienzan en 1 y aumentan a través de ciertos valores más o menos «a medias» y luego disminuyen a través de estos mismos valores de vuelta a 1.
Exploremos más los coeficientes. Supongamos que queremos encontrar una expansión de (a + b)6. Los patrones que acabamos de observar indican que hay 7 términos en la expansión:
a6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6.
¿Cómo podemos determinar el valor de cada coeficiente, ci? Podemos hacerlo de dos maneras. El primer método consiste en escribir los coeficientes en una matriz triangular, como se indica a continuación. Esto se conoce como el triángulo de Pascal: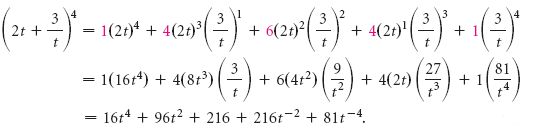
Hay muchos patrones en el triángulo. Encuentra todos los que puedas.
Tal vez hayas descubierto una forma de escribir la siguiente fila de números, dados los números de la fila de arriba. Siempre hay 1’s en el exterior. Cada número restante es la suma de los dos números de arriba. Intentemos encontrar una expansión para (a + b)6 añadiendo otra fila utilizando los patrones que hemos descubierto:
Vemos que en la última fila
el 1º y el último número son 1;
el 2º número es 1 + 5, o 6;
el 3º número es 5 + 10, o 15;
el 4º número es 10 + 10, o 20;
el 5º número es 10 + 5, o 15; y
el 6º número es 5 + 1, o 6.
Así, la expansión de (a + b)6 es
(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Para encontrar una expansión de (a + b)8, completamos dos filas más del triángulo de Pascal: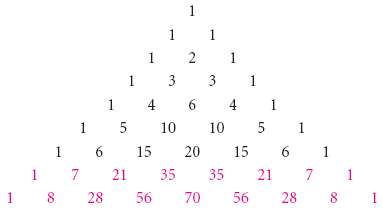
Así la expansión de es
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Podemos generalizar nuestros resultados de la siguiente manera.
El teorema del binomio utilizando el triángulo de Pascal
Para cualquier binomio a + b y cualquier número natural n,
(a + b)n = c0anb0 + c1an-1b1 + c2an-2b2 + …. + cn-1a1bn-1 + cna0bn,
donde los números c0, c1, c2,…., cn-1, cn son de la (n + 1)-primera fila del triángulo de Pascal.
Ejemplo 1 Expandir: (u – v)5.
Solución Tenemos (a + b)n, donde a = u, b = -v, y n = 5. Utilizamos la 6ª fila del triángulo de Pascal:
1 5 10 10 5 1
Entonces tenemos
(u – v)5 = 5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5.
Nota que los signos de los términos alternan entre + y -. Cuando la potencia de -v es impar, el signo es -.
Ejemplo 2 Expandir: (2t + 3/t)4.
Solución Tenemos (a + b)n, donde a = 2t, b = 3/t, y n = 4. Usamos la 5ª fila del triángulo de Pascal:
1 4 6 4 1
Entonces tenemos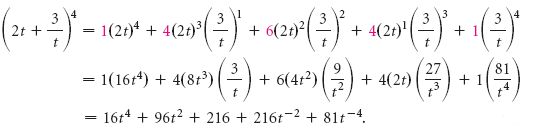
Expansión del binomio usando la notación factorial
Supongamos que queremos encontrar la expansión de (a + b)11. El inconveniente de utilizar el triángulo de Pascal es que debemos calcular todas las filas anteriores del triángulo para obtener la fila necesaria para la expansión. El siguiente método evita esto. También nos permite encontrar un término específico -por ejemplo, el octavo término- sin tener que calcular todos los demás términos de la expansión. Este método es útil en cursos como las matemáticas finitas, el cálculo y la estadística, y utiliza la notación del coeficiente binomial 
.
Podemos replantear el teorema del binomio como sigue.
El teorema del binomio usando la notación factorial
Para cualquier binomio (a + b) y cualquier número natural n,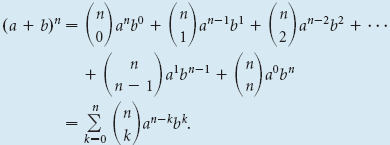
.
El teorema del binomio se puede demostrar por inducción matemática. (VerEjercicio 63.) Esta forma muestra por qué se llama coeficiente binomial.
Ejemplo 3 Expandir: (x2 – 2y)5.
Solución Tenemos (a + b)n,donde a = x2, b = -2y, y n = 5. Entonces, utilizando el teorema del binomio, tenemos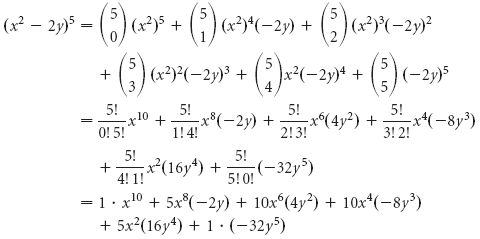
Finalmente (x2 – 2y)5 = x10 – 10x8y + 40x6y2 – 80x4y3 + 80x2y4 – 32y5.
Ejemplo 4 Expandir: (2/x + 3√x)4.
Solución Tenemos (a + b)n, donde a = 2/x, b = 3√x, y n = 4. Entonces, utilizando el teorema del binomio, tenemos
Finalmente (2/x + 3√x)4 = 16/x4 + 96/x5/2 + 216/x + 216×1/2 + 81×2.
Encontrar un término concreto
Supongamos que queremos determinar sólo un término concreto de una expansión. El método que hemos desarrollado nos permitirá encontrar dicho término sin necesidad de calcular todas las filas del triángulo de Pascal o todos los coeficientes anteriores.
Nótese que en el teorema del binomio, 
nos da el primer término,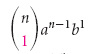 
nos da el segundo término, 
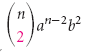nos da el tercer término, y así sucesivamente. Esto se puede generalizar de la siguiente manera.
Hallar el (k + 1)-primer término
El (k + 1)-primer término de (a + b)n es 
.
Ejemplo 5 Hallar el 5º término en la expansión de (2x – 5y)6.
Solución Primero, observamos que 5 = 4 + 1. Por tanto, k = 4, a = 2x, b = -5y, y n = 6. Entonces el 5º término de la expansión es
Ejemplo 6 Encuentra el 8º término de la expansión de (3x – 2)10.
Solución Primero, observamos que 8 = 7 + 1. Por tanto, k = 7, a = 3x, b = -2 y n = 10. Entonces el 8º término de la expansión es
Número total de subconjuntos
Supongamos que un conjunto tiene n objetos. El número de subconjuntos que contienen k elementos . El número total de subconjuntos de un conjunto es el número de subconjuntos con 0 elementos, más el número de subconjuntos con 1 elemento, más el número de subconjuntos con 2 elementos, y así sucesivamente. El número total de subconjuntos de un conjunto con n elementos es
.
Consideremos ahora la expansión de (1 + 1)n:
.
Así, el número total de subconjuntos es (1 + 1)n, o sea 2n. Hemos demostrado lo siguiente.
Número total de subconjuntos
El número total de subconjuntos de un conjunto con n elementos es 2n.
Ejemplo 7 El conjunto {A, B, C, D, E} tiene ¿cuántos subconjuntos?
Solución El conjunto tiene 5 elementos, por lo que el número de subconjuntos es 25, o 32.
Ejemplo 8 Wendy’s, una cadena nacional de restaurantes, ofrece los siguientes aderezos para sus hamburguesas:
{sup, mostaza, mayonesa, tomate, lechuga, cebolla, pepinillo, relish, queso}.
¿Cuántos tipos diferentes de hamburguesas puede servir Wendy’s, excluyendo el tamaño de la hamburguesa o el número de hamburguesas?
Solución Los aderezos de cada hamburguesa son los elementos de un subconjunto del conjunto de todos los aderezos posibles, siendo el conjunto vacío una hamburguesa normal. El número total de hamburguesas posibles es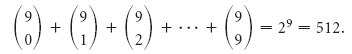
Por tanto, Wendy’s sirve hamburguesas de 512 formas diferentes.