La distribución normal estándar también puede ser útil para calcular los percentiles
. Por ejemplo, la mediana es el percentil 50, el primer cuartil es el percentil 25 y el tercer cuartil es el percentil 75. En algunos casos puede ser interesante calcular otros percentiles, por ejemplo el 5º o el 95º. La fórmula siguiente se utiliza para calcular los percentiles de una distribución normal.
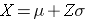
Donde μ es la media y σ es la desviación estándar de la variable X, y Z es el valor de la distribución normal estándar para el percentil deseado.
Ejemplo:
- La media del IMC para hombres de 60 años es de 29 con una desviación estándar de 6.
- La media del IMC para mujeres de 60 años la media es de 28 con una desviación estándar de 7.
¿Cuál es el percentil 90 del IMC para los hombres?
El percentil 90 es el IMC que tiene el 90% de los IMC por debajo y el 10% por encima, como se ilustra en la figura siguiente.
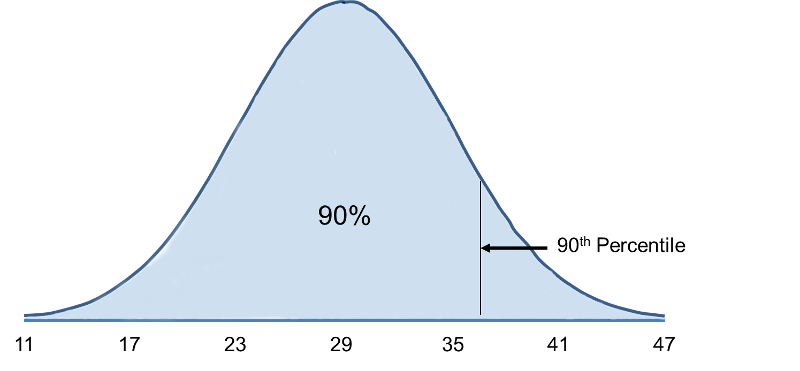
Para calcular el percentil 90, utilizamos la fórmula X=μ + Zσ, y usaremos la tabla de distribución normal estándar, excepto que trabajaremos en sentido contrario. Anteriormente comenzamos con una «X» determinada y utilizamos la tabla para encontrar la probabilidad. Sin embargo, en este caso queremos empezar con una probabilidad del 90% y encontrar el valor de «X» que la representa.
Así que empezamos yendo al interior de la tabla de distribución normal estándar para encontrar el área bajo la curva más cercana a 0,90, y a partir de ahí podemos determinar la puntuación Z correspondiente. Una vez que tenemos esto podemos utilizar la ecuación X=μ + Zσ, porque ya sabemos que la media y la desviación estándar son 29 y 6, respectivamente.
Cuando vamos a la tabla, encontramos que el valor 0,90 no está ahí exactamente, sin embargo, los valores 0,8997 y 0,9015 sí están y corresponden a valores Z de 1,28 y 1,29, respectivamente (es decir, el 89,97% del área bajo la curva normal estándar está por debajo de 1,28). El valor Z exacto que mantiene el 90% de los valores por debajo es 1,282, que se determinó a partir de una tabla de probabilidades normales estándar con mayor precisión.
Usando Z=1,282 el percentil 90 del IMC para los hombres es: X = 29 + 1,282(6) = 36,69.
Interpretación: El noventa por ciento de los IMC de los hombres de 60 años están por debajo de 36,69. El diez por ciento de los IMC de los hombres de 60 años están por encima de 36,69
¿Cuál es el percentil 90 del IMC entre las mujeres de 60 años? Recordemos que la media del IMC de las mujeres de 60 años la media es de 28 con una desviación estándar de 7.
Respuesta
La siguiente tabla muestra los valores Z de los percentiles más utilizados.
|
Percentil |
Z |
|---|---|
|
1º |
-2.326 |
|
2.5º |
-1.960 |
|
5ª |
-1.645 |
|
10º |
-1.282 |
|
25º |
-0.675 |
|
50º |
0 |
|
75º |
0.675 |
|
90º |
1.282 |
|
95º |
1.645 |
|
97,5º |
1.960 |
|
99º |
2.326 |
Los percentiles de altura y peso son utilizados por los pediatras para evaluar el desarrollo en relación con los niños del mismo sexo y edad. Por ejemplo, si el peso de un niño para su edad es extremadamente bajo puede ser un indicio de desnutrición. Las tablas de crecimiento están disponibles en http://www.cdc.gov/growthcharts/.
Para las niñas de corta edad, la longitud corporal media a los 10 meses es de 72 centímetros con una desviación estándar de 3 centímetros. Supongamos que una niña de 10 meses tiene una longitud medida de 67 centímetros. Cómo se compara su longitud con la de otras niñas de 10 meses?
Respuesta
Un recuento sanguíneo completo (CBC) es una prueba comúnmente realizada. Uno de los componentes del hemograma es el recuento de glóbulos blancos (WBC), que puede ser indicativo de infección si el recuento es alto. Los recuentos de glóbulos blancos tienen una distribución aproximadamente normal en personas sanas, con una media de 7.550 glóbulos blancos por mm3 (es decir, por microlitro) y una desviación estándar de 1.085. ¿Qué proporción de sujetos tienen recuentos de glóbulos blancos superiores a 9000?
Respuesta