Aquí tienes una pregunta típica de libro de texto. Tu coche se ha quedado sin gasolina. Con cuánta fuerza necesitas empujarlo para acelerarlo a una velocidad determinada?
La respuesta proviene de la segunda ley del movimiento de Newton:
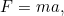 |
. |
donde  es la aceleración,
es la aceleración, 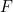 es la fuerza y
es la fuerza y 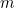 es la masa. Esta ley maravillosamente sencilla, aunque sutil, permite describir el movimiento de todo tipo y, por tanto, puede, al menos en teoría, responder a casi cualquier pregunta que un físico quiera hacerse sobre el mundo.
es la masa. Esta ley maravillosamente sencilla, aunque sutil, permite describir el movimiento de todo tipo y, por tanto, puede, al menos en teoría, responder a casi cualquier pregunta que un físico quiera hacerse sobre el mundo.

La ecuación de Schrödinger lleva el nombre de Erwin Schrödinger, 1887-1961.
Olas y partículas
«En la mecánica clásica describimos el estado de un sistema físico mediante la posición y el momento», explica Nazim Bouatta, físico teórico de la Universidad de Cambridge. Por ejemplo, si tenemos una mesa llena de bolas de billar en movimiento y conocemos la posición y el momento (es decir, la masa por la velocidad) de cada bola en un momento determinado  , entonces sabemos todo lo que hay que saber sobre el sistema en ese momento
, entonces sabemos todo lo que hay que saber sobre el sistema en ese momento 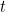 : dónde está todo, hacia dónde va todo y a qué velocidad. «El tipo de pregunta que nos hacemos entonces es: si conocemos las condiciones iniciales de un sistema, es decir, conocemos el sistema en el momento
: dónde está todo, hacia dónde va todo y a qué velocidad. «El tipo de pregunta que nos hacemos entonces es: si conocemos las condiciones iniciales de un sistema, es decir, conocemos el sistema en el momento 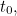 ¿cuál es la evolución dinámica de este sistema? Y para ello utilizamos la segunda ley de Newton. En la mecánica cuántica nos hacemos la misma pregunta, pero la respuesta es complicada porque la posición y el momento ya no son las variables adecuadas para describir.»
¿cuál es la evolución dinámica de este sistema? Y para ello utilizamos la segunda ley de Newton. En la mecánica cuántica nos hacemos la misma pregunta, pero la respuesta es complicada porque la posición y el momento ya no son las variables adecuadas para describir.»
El problema es que los objetos que la mecánica cuántica intenta describir no siempre se comportan como pequeñas bolas de billar. A veces es mejor pensar en ellos como ondas. «Tomemos el ejemplo de la luz. Newton, además de su trabajo sobre la gravedad, también se interesó por la óptica», dice Bouatta. «Según Newton, la luz se describía mediante partículas. Pero después, tras el trabajo de muchos científicos, incluida la comprensión teórica proporcionada por James Clerk Maxwell, descubrimos que la luz se describía mediante ondas».
Pero en 1905 Einstein se dio cuenta de que la imagen de las ondas tampoco era del todo correcta. Para explicar el efecto fotoeléctrico (véase el artículo de Plus La crisis de identidad de la luz) hay que pensar en un haz de luz como un flujo de partículas, que Einstein denominó fotones. El número de fotones es proporcional a la intensidad de la luz, y la energía E de cada fotón es proporcional a su frecuencia f:
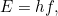 |
Aquí  es la constante de Planck, un número increíblemente pequeño que lleva el nombre del físico Max Planck, quien ya había adivinado esta fórmula en 1900 en su trabajo sobre la radiación del cuerpo negro.»Así que nos enfrentamos a la situación de que a veces la forma correcta de describir la luz era como ondas y a veces era como partículas», dice Bouatta.
es la constante de Planck, un número increíblemente pequeño que lleva el nombre del físico Max Planck, quien ya había adivinado esta fórmula en 1900 en su trabajo sobre la radiación del cuerpo negro.»Así que nos enfrentamos a la situación de que a veces la forma correcta de describir la luz era como ondas y a veces era como partículas», dice Bouatta.

El experimento de la doble rendija: La imagen superior muestra el patrón de interferencia creado por las ondas que pasan a través de las rendijas, la imagen del medio muestra lo que se esperaría ver cuando se disparan partículas a través de las rendijas, y la imagen inferior muestra lo que realmente sucede cuando se disparan partículas como los electrones a través de las rendijas: se obtiene el patrón de interferencia que se espera de las ondas, pero los electrones se registran como si llegaran como partículas.
El resultado de Einstein enlaza con el antiguo esfuerzo, iniciado en el siglo XVII por Christiaan Huygens y explorado de nuevo en el siglo XIX por William Hamilton: unificar la física de la óptica (que trataba sobre las ondas) y la mecánica (que trataba sobre las partículas). Inspirado por el comportamiento esquizofrénico de la luz, el joven físico francés Louis deBroglie dio un paso espectacular en este camino: postuló que no sólo la luz, sino también la materia, sufrían la llamada dualidad onda-partícula. Los diminutos componentes de la materia, como los electrones, también se comportan como partículas en algunas situaciones y como ondas en otras.
La idea de Broglie, que anunció en la década de 1920, no se basaba en pruebas experimentales, sino que surgía de consideraciones teóricas inspiradas en la teoría de la relatividad de Einstein. Pero las pruebas experimentales no tardaron en llegar. A finales de la década de 1920, los experimentos con partículas que se dispersaban en un cristal confirmaron la naturaleza ondulatoria de los electrones (véase el artículo del Plus La incertidumbre cuántica).
Una de las demostraciones más famosas de la dualidad onda-partícula es el experimento de la doble rendija. En él, los electrones (u otras partículas como los fotones o los neutrones) se disparan uno a uno sobre una pantalla que contiene dos rendijas. Detrás de la pantalla hay una segunda que puede detectar dónde acaban los electrones que han pasado por las rendijas. Si los electrones se comportaran como partículas, se esperaría que se amontonaran alrededor de dos líneas rectas detrás de las dos rendijas. Pero lo que se ve en la pantalla del detector es un patrón de interferencia: el patrón que se obtendría si los electrones fueran ondas, cada una de las cuales pasaría por las dos rendijas a la vez y luego se interferiría a sí misma al extenderse de nuevo por el otro lado. Sin embargo, en la pantalla del detector, los electrones se registran tal y como cabría esperar: como partículas. Se trata de un resultado muy extraño, pero que se ha reproducido muchas veces: simplemente tenemos que aceptar que el mundo funciona así.
Ecuación de Schrödinger
La nueva imagen radical propuesta por de Broglie requería una nueva física. Cómo se ve matemáticamente una onda asociada a una partícula? Einstein ya había relacionado la energía 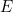 de un fotón con la frecuencia
de un fotón con la frecuencia 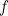 de la luz, que a su vez está relacionada con la longitud de onda
de la luz, que a su vez está relacionada con la longitud de onda 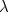 mediante la fórmula
mediante la fórmula 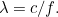 Aquí
Aquí  es la velocidad de la luz. Utilizando los resultados de la teoría de la relatividad también es posible relacionar la energía de un fotón con su momento. Si juntamos todo esto obtenemos la relación
es la velocidad de la luz. Utilizando los resultados de la teoría de la relatividad también es posible relacionar la energía de un fotón con su momento. Si juntamos todo esto obtenemos la relación
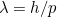
entre la longitud de onda del fotón 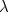 y el momento
y el momento 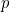
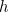 de nuevo es la constante de Planck).
de nuevo es la constante de Planck).
Siguiendo con esto, de Broglie postuló que la misma relación entre la longitud de onda y el momento debería ser válida para cualquier partícula.
En este punto es mejor suspender tu intuición sobre lo que realmente significa decir que una partícula se comporta como una onda (lo veremos en el tercer artículo)y seguir con las matemáticas.
En la mecánica clásica la evolución en el tiempo de una onda, por ejemplo una onda sonora o una onda de agua, se describe mediante una ecuación de onda: una ecuación diferencial cuya solución es una función de onda, que te da la forma de la onda en cualquier momento 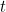 (sujeta a unas condiciones de contorno adecuadas).
(sujeta a unas condiciones de contorno adecuadas).
Por ejemplo, supongamos que tenemos ondas viajando a través de una cuerda que se estira a lo largo del eje  y vibra en el plano
y vibra en el plano 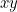 . Para describir la onda completamente, necesitas encontrar el desplazamiento
. Para describir la onda completamente, necesitas encontrar el desplazamiento 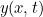 de la cuerda en la dirección
de la cuerda en la dirección 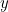 en cada punto
en cada punto  y en cada momento
y en cada momento 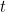 . Utilizando la segunda ley del movimiento de Newton es posible demostrar que
. Utilizando la segunda ley del movimiento de Newton es posible demostrar que 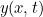 obedece a la siguiente ecuación de onda:
obedece a la siguiente ecuación de onda:
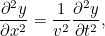 |
. |
donde  es la velocidad de las ondas.
es la velocidad de las ondas.

Una instantánea en el tiempo de una cuerda que vibra en el plano xy. La onda mostrada aquí está descrita por la función coseno.
Una solución general 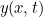 de esta ecuación es bastante complicada, ya que refleja el hecho de que la cuerda puede estar contoneándose de todo tipo de formas, y que se necesita más información (condiciones iniciales y condiciones de contorno) para saber exactamente de qué tipo de movimiento se trata. Pero como ejemplo, la función
de esta ecuación es bastante complicada, ya que refleja el hecho de que la cuerda puede estar contoneándose de todo tipo de formas, y que se necesita más información (condiciones iniciales y condiciones de contorno) para saber exactamente de qué tipo de movimiento se trata. Pero como ejemplo, la función
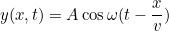 |
. |
Describe una onda que viaja en la dirección positiva  -con una frecuencia angular
-con una frecuencia angular 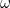 , así que, como era de esperar, es una posible solución a la ecuación de onda.
, así que, como era de esperar, es una posible solución a la ecuación de onda.
Por analogía, debería existir una ecuación de onda que rigiera la evolución de las misteriosas «ondas de materia», sean las que sean, a lo largo del tiempo. Su solución sería una función de onda 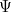 (pero resístete a pensar que describe una onda real) que te dice todo lo que hay que saber sobre tu sistema cuántico -por ejemplo, una sola partícula moviéndose en una caja- en cualquier momento
(pero resístete a pensar que describe una onda real) que te dice todo lo que hay que saber sobre tu sistema cuántico -por ejemplo, una sola partícula moviéndose en una caja- en cualquier momento 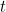 . Fue el físico austriaco Erwin Schrödinger quien ideó esta ecuación en 1926. Para una sola partícula que se mueve en tres dimensiones la ecuación puede escribirse como
. Fue el físico austriaco Erwin Schrödinger quien ideó esta ecuación en 1926. Para una sola partícula que se mueve en tres dimensiones la ecuación puede escribirse como
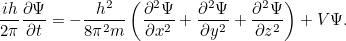 |
Aquí 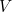 es la energía potencial de la partícula (una función de
es la energía potencial de la partícula (una función de 
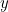
 y
y 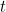
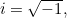
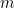 es la masa de la partícula y
es la masa de la partícula y 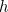 es la constante de Planck. La solución de esta ecuación es la función de onda
es la constante de Planck. La solución de esta ecuación es la función de onda 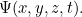
En algunas situaciones la energía potencial no depende del tiempo 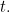 En este caso, a menudo podemos resolver el problema considerando la versión más sencilla de la ecuación de Schrödinger independiente del tiempo para una función
En este caso, a menudo podemos resolver el problema considerando la versión más sencilla de la ecuación de Schrödinger independiente del tiempo para una función 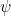 que sólo depende del espacio, es decir.e.
que sólo depende del espacio, es decir.e. 
 |
. |
donde  es la energía total de la partícula. La solución
es la energía total de la partícula. La solución 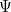 de la ecuación completa es entonces
de la ecuación completa es entonces
 |
Estas ecuaciones se aplican a una partícula que se mueve en tres dimensiones, pero tienen contrapartes que describen un sistema con cualquier número de partículas. Y en lugar de formular la función de onda como una función de posición y tiempo, también se puede formular como una función de momento y tiempo.
Entre la incertidumbre
Veremos cómo resolver la ecuación de Schrödinger para un ejemplo sencilloen el segundo artículo, y también que su solución es efectivamente similar a la ecuación matemática que describe una onda.
¿Pero qué significa realmente esta solución? No te da una localización precisa de tu partícula en un momento determinado  , por lo que no te da la trayectoria de una partícula en el tiempo. Más bien es una función que, en un momento dado
, por lo que no te da la trayectoria de una partícula en el tiempo. Más bien es una función que, en un momento dado  te da un valor
te da un valor 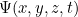 para todas las posibles ubicaciones
para todas las posibles ubicaciones 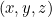 . ¿Qué significa este valor? En 1926, el físico Max Born propuso una interpretación probabilística. Postuló que el cuadrado del valor absoluto de la función de onda,
. ¿Qué significa este valor? En 1926, el físico Max Born propuso una interpretación probabilística. Postuló que el cuadrado del valor absoluto de la función de onda,
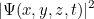 |
|
te da la densidad de probabilidad para encontrar la partícula en la posición 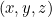 en el tiempo
en el tiempo 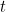 . En otras palabras, la probabilidad de que la partícula se encuentre en una región
. En otras palabras, la probabilidad de que la partícula se encuentre en una región 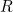 en el tiempo
en el tiempo 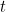 viene dada por la integral
viene dada por la integral
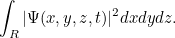 |
id=»3231265849″> |
(Puedes encontrar más información sobre las densidades de probabilidad en cualquier introducción a la teoría de la probabilidad, por ejemplo aquí.)

Werner Heisenberg, 1901-1976.
«Si creemos en esta imagen de incertidumbre, entonces tenemos que aceptar un relato probabilístico porque no tenemos respuestas exactas a preguntas como ‘¿dónde está el electrón en el momento 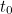 ?'», dice Bouatta. En otras palabras, todo lo que puedes esperar de la representación matemática de un estado cuántico, de la función de onda, es que te dé una probabilidad.
?'», dice Bouatta. En otras palabras, todo lo que puedes esperar de la representación matemática de un estado cuántico, de la función de onda, es que te dé una probabilidad.
Si la función de onda tiene o no alguna interpretación física era y sigue siendo una cuestión delicada. «La pregunta era: tenemos esta función de onda, pero ¿realmente pensamos que hay ondas que se propagan en el espacio y el tiempo?», dice Bouatta. «De Broglie, Schrödinger y Einstein intentaban dar una explicación realista, que es como una onda de luz, por ejemplo, que se propaga en el vacío. Pero, Wolfgang Pauli, Werner Heisenberg y Niels Bohr estaban en contra de esta imagen realista. Para ellos la función de onda era sólo una herramienta para calcular probabilidades». Veremos más de cerca la interpretación de la función de onda en el tercer artículo de esta serie.
¿Funciona?

Louis de Broglie, 1892-1987.
¿Por qué deberíamos creer en este montaje tan fantástico? En este artículo hemos presentado la ecuación de Schrödinger como si la hubiéramos sacado del aire, pero ¿de dónde procede realmente? ¿Cómo la concibió Schrödinger? El famoso físico Richard Feynman se planteó esta pregunta de forma afable: «¿De dónde lo sacamos? No es posible derivarlo de nada conocido. Salió de la mente de Schrödinger».
Sin embargo, la ecuación se ha mantenido en todos los experimentos hasta ahora. «Es la ecuación másfundamental de la mecánica cuántica», dice Bouatta. «Es el punto de partida de cualquier sistema mecánico cuántico que queramos describir: electrones, protones, neutrones, lo que sea». El mayor éxito de la ecuación, que fue también una de las motivaciones de Schrödinger, fue describir un fenómeno que ayudó a dar a luz a la mecánica cuántica en primer lugar: el espectro energético discreto del átomo de hidrógeno. Según el modelo satómico de Ernest Rutherford, la frecuencia de la radiación emitida por átomos como el hidrógeno debería variar continuamente. Sin embargo, los experimentos demostraron que no es así: el átomo de hidrógeno sólo emite radiación a determinadas frecuencias, y hay un salto cuando la frecuencia cambia. Este descubrimiento se enfrentó a la sabiduría convencional, que respaldaba una máxima establecida por el filósofo y matemático del siglo XVII Gottfried Leibniz: «la naturaleza no da saltos».
En 1913 Niels Bohr propuso un nuevo modelo atómico en el que los electrones se limitan a determinados niveles de energía. Schrödinger aplicó su ecuación al átomo de hidrógeno y descubrió que sus soluciones reproducían exactamente los niveles de energía estipulados por Bohr. «Este fue un resultado asombroso, y uno de los primeros grandes logros de la ecuación de Schrödinger», dice Bouatta.
Con innumerables éxitos experimentales en su haber, la ecuación de Schrödinger se ha convertido en el análogo establecido de la segunda ley de movimiento de Newton para la mecánica cuántica. Veamos ahora la ecuación de Schrödinger en acción, utilizando el sencillo ejemplo de una partícula que se mueve en una caja. También exploraremos otra extraña consecuencia de la ecuación llamada tunelización cuántica.
Lee el siguiente artículo: La ecuación de Schrödinger – en acción
Pero si no le apetece hacer las cuentas puede pasar directamente al tercer artículo que explora la interpretación de la función de onda.
Acerca de este artículo
Nazim Bouatta es un investigador postdoctoral en Fundamentos de la Física en la Universidad de Cambridge.
Marianne Freiberger es editora de Plus. Entrevistó a Bouatta en Cambridge en mayo de 2012. También desea agradecer a Jeremy Butterfield, filósofo de la física en la Universidad de Cambridge, y a Tony Short, investigador de la Royal Society en Fundamentos de la Física Cuántica en la Universidad de Cambridge, su ayuda en la redacción de estos artículos.