Objetivos de aprendizaje
- Definir la vida media.
- Determinar la cantidad de sustancia radiactiva que queda después de un número determinado de vidas medias.
Si un isótopo dado es radiactivo o no, es una característica de ese isótopo en particular. Algunos isótopos son estables indefinidamente, mientras que otros son radiactivos y decaen mediante una forma de emisión característica. A medida que pasa el tiempo, cada vez habrá menos isótopos radiactivos, y el nivel de radiactividad disminuye. Un aspecto interesante y útil de la desintegración radiactiva es la vida media. La vida media de un isótopo radiactivo es la cantidad de tiempo que tarda la mitad del isótopo radiactivo en descomponerse. La vida media de un isótopo radiactivo específico es constante; no se ve afectada por las condiciones y es independiente de la cantidad inicial de ese isótopo.
Considere el siguiente ejemplo. Supongamos que tenemos 100,0 g de 3H (tritio, un isótopo radiactivo del hidrógeno). Tiene un periodo de semidesintegración de 12,3 años. Después de 12,3 años, la mitad de la muestra habrá decaído a 3He mediante la emisión de una partícula beta, de modo que sólo quedarán 50,0 g del 3H original. Después de otros 12,3 años, es decir, un total de 24,6 años, otra mitad del 3H restante se habrá desintegrado, dejando 25,0 g de 3H. Después de otros 12,3 años -ahora un total de 36,9 años- otra mitad del 3H restante se habrá descompuesto, dejando 12,5 g de 3H. Esta secuencia de eventos se ilustra en la Figura \(\PageIndex{1}).
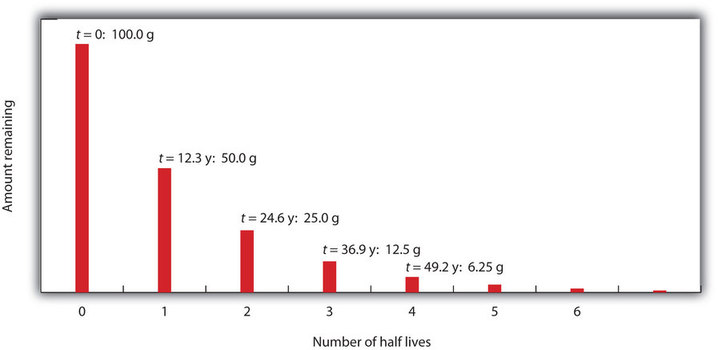
Podemos determinar la cantidad de un isótopo radiactivo que queda después de un número dado de vidas medias utilizando la siguiente expresión:
donde n es el número de vidas medias. Esta expresión funciona incluso si el número de semividas no es un número entero.
Ejemplo \(\PageIndex{1}): Flúor-20
El periodo de semidesintegración del 20F es de 11,0 s. Si una muestra contiene inicialmente 5,00 g de 20F, ¿cuánto 20F queda después de 44,0 s?
Solución
Si comparamos el tiempo transcurrido con el periodo de semidesintegración del isótopo, observamos que 44,0 s son exactamente 4 periodos de semidesintegración, por lo que podemos utilizar la ecuación \ref{E1} con \(n = 4\). Sustituyendo y resolviendo resulta lo siguiente:
&=5.00\: g \times \dfrac{1}{16} &=0.313: g \Nfinal{align*}]
Queda menos de un tercio de gramo de 20F.
Ejercicio \N(\NIndex{1}): Titanio-44
La vida media del 44Ti es de 60,0 y. Una muestra contiene inicialmente 0,600 g de 44Ti. ¿Cuánto 44Ti queda después de 180,0 y?
Respuesta
0,075 g.
Las vidas medias de los isótopos van desde fracciones de microsegundo hasta miles de millones de años. La tabla \(\PageIndex{1}) enumera las vidas medias de algunos isótopos.
| Isótopo | Vida mediaVida |
|---|---|
| 3H | 12.3 y |
| 14C | 5,730 y |
| 40K | 1.26 × 109 y | 51Cr | 27,70 d | 90Sr | 29.1 y |
| 131I | 8,04 d | 222Rn | 3.823 d | 235U | 7,04 × 108 y | 238U | 4.47 × 109 y | 241Am | 432,7 y | 248Bk | 23.7 h | 260Sg | 4 ms |
Ejemplo \(\PageIndex{2}\): Yodo-125
El isótopo \(\ce{I})-125 se utiliza en ciertos procedimientos de laboratorio y tiene una vida media de 59,4 días. Si la actividad inicial de una muestra de \ce{I})-125 es de \c \text{contados por minuto (cpm)}}, ¿cuánta actividad habrá en 178,2 días?
Solución
Empezamos por determinar cuántas vidas medias representan 178.2 días:
Entonces simplemente contamos la actividad:
Asegúrate de tener en cuenta que el recuento inicial es en el tiempo cero \(\left( t_0 \right)\Ny restamos de ese recuento en la primera vida media. La segunda semivida tiene una actividad de la mitad del recuento anterior (no del recuento inicial).
La ecuación \(\ref{Eq1}\a) se puede utilizar para calcular la cantidad de radiactividad que queda después de un tiempo determinado:
donde \(N_t =\a) actividad en el tiempo \a(t\a) y \a(N_0 =\a) actividad inicial en el tiempo \a(t = 0\a).
Si tenemos una actividad inicial de \(42.000 \: \text{cpm}\), ¿cuál será la actividad después de cuatro vidas medias?
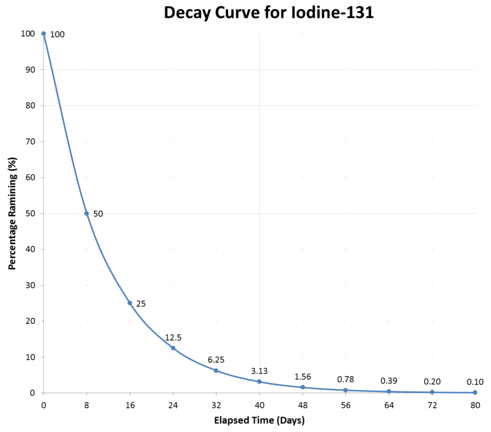
Curva de desintegración radiactiva típica.
El gráfico anterior ilustra una curva de desintegración típica para el \ce{I}-125\). La actividad disminuye a la mitad durante cada vida media sucesiva.
Ejercicio \(\PageIndex{2})
Una muestra de \(\ce{Ac})-225 contenía originalmente 80 gramos y después de 50 días sólo quedan 2,5 gramos del \ce{Ac})-225 original. ¿Cuál es la vida media de \(\ce{Ac})-225?
Respuesta
10 días
Mirando más de cerca: vidas medias de los elementos radiactivos
Mucha gente piensa que la vida media de un elemento radiactivo representa la cantidad de tiempo que un elemento es radiactivo. En realidad, es el tiempo necesario para que la mitad -no todo- del elemento se desintegre radiactivamente. En ocasiones, sin embargo, el elemento hijo también es radiactivo, por lo que también hay que tener en cuenta su radiactividad.
La vida útil esperada de un detector de humo de tipo ionización (descrito en el ensayo inicial) es de unos 10 años. En ese tiempo, el americio-241, que tiene una vida media de unos 432 años, pierde menos del 4% de su radiactividad. Una vida media de 432 años puede parecernos larga, pero no es muy larga en cuanto a vidas medias. El uranio-238, el isótopo más común del uranio, tiene una vida media de unos 4,5 × 109 años, mientras que el torio-232 tiene una vida media de 14 × 109 años.
Por otro lado, algunos núcleos tienen vidas medias extremadamente cortas, lo que supone un reto para los científicos que los estudian. El isótopo más longevo del lawrencio, el 262Lr, tiene una vida media de 3,6 h, mientras que el isótopo más corto del lawrencio, el 252Lr, tiene una vida media de 0,36 s. En el momento de escribir este artículo, el átomo más grande jamás detectado tiene el número atómico 118, el número de masa 293 y una vida media de 120 ns. ¿Te imaginas lo rápido que debe hacerse un experimento para determinar las propiedades de elementos que existen durante tan poco tiempo?
Las claves
- Los procesos radiactivos naturales se caracterizan por una vida media, el tiempo que tarda la mitad del material en decaer radiactivamente.
- La cantidad de material que queda después de un cierto número de vidas medias puede calcularse fácilmente.
Ejercicios de repaso de conceptos
- Define la vida media.
- Describe una forma de determinar la cantidad de isótopo radiactivo que queda tras un número determinado de vidas medias.
Respuestas
- La vida media es la cantidad de tiempo necesaria para que la mitad de un material radiactivo se desintegre.
- Toma la mitad de la cantidad inicial por cada vida media de tiempo transcurrida