Un test t indipendente a due campioni può essere eseguito su dati campione di una variabile numerica di risultato normalmente distribuita per determinare se la sua media differisce tra due gruppi indipendenti. Per esempio, potremmo vedere se il GPA medio differisce tra gli studenti del primo e dell’ultimo anno di college raccogliendo un campione di ogni gruppo di studenti e registrando i loro GPA.
Ipotesi:
Ho: La media della popolazione di un gruppo è uguale alla media della popolazione dell’altro gruppo, o μ1 = μ2
HA: La media della popolazione di un gruppo non è uguale alla media della popolazione dell’altro gruppo, o μ1 ≠ μ2
Questo test può anche essere condotto con un’ipotesi alternativa direzionale:
Ho: La media della popolazione di un gruppo è uguale alla media della popolazione dell’altro gruppo, o μ1 = μ2
Ha: La media della popolazione di un gruppo è maggiore della media della popolazione dell’altro gruppo, o μ1 > μ2
La statistica del test per un test t indipendente a due campioni è calcolata prendendo la differenza tra le due medie campionarie e dividendola per l’errore standard stimato unpooled o pooled. L’errore standard stimato è una misura aggregata della quantità di variazione in entrambi i gruppi.
Equazioni rilevanti:
Gradi di libertà: Varia a seconda delle condizioni, ma la regola di base per i calcoli manuali è la più piccola tra n1 – 1 e n2 – 1, dove n è la dimensione del campione per ogni gruppo.
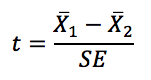
Assunzioni:
- Campioni casuali
- Osservazioni indipendenti
- La popolazione di ogni gruppo è distribuita normalmente.
- Le varianze della popolazione sono uguali.
Se la terza assunzione non è soddisfatta, il test alternativo è il Mann-Whitney U-Test, che può essere eseguito per vedere se c’è una differenza tra due gruppi per una variabile con qualsiasi tipo di distribuzione.
Se la quarta assunzione è soddisfatta, allora l’errore standard stimato in comune viene utilizzato nel calcolo della statistica del test. Se la quarta ipotesi non è soddisfatta, allora viene utilizzato l’errore standard stimato non aggregato, più conservativo (e il test viene chiamato “Test di Welch”).
Esempio 1: video sul calcolo manuale
Questo esempio esamina il numero medio di ore dormite dagli studenti maschi rispetto alle studentesse.


Conclusione del campione: Con t(df=40)=1,73, che era più estremo del nostro valore critico di 1,68, questi dati forniscono la prova che le studentesse dormono di più, in media, rispetto agli studenti maschi.
Esempio 2: Come eseguire in Excel 2016
Alcune di queste analisi richiedono che l’add-in Data Analysis ToolPak in Excel sia attivato. Per le istruzioni su come condurre questa analisi nelle versioni precedenti di Excel, visita https://stat.utexas.edu/videos
In questo tutorial, determinerai se maschi e femmine differiscono nel loro livello di felicità.
NOTA: In questo video, il test t è condotto assumendo varianze disuguali (test di Welch).
Dataset usato nel video
Direzioni PDF corrispondenti al video
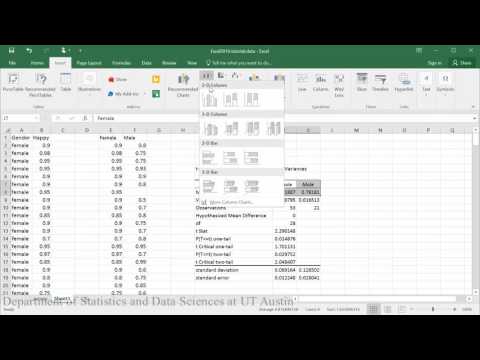

Conclusione del campione: Con t(df=28)=2.29, p<0.05, questi dati forniscono la prova che le studentesse sono più felici, in media, degli studenti maschi.
Esempio 3: Come eseguire in RStudio
Questo esempio esamina il numero medio di ore dormite dagli studenti maschi rispetto alle studentesse.
NOTA: In questo video, il t-test è condotto assumendo varianze ineguali (test di Welch).
Dataset usato nel video
File di script R usato nel video
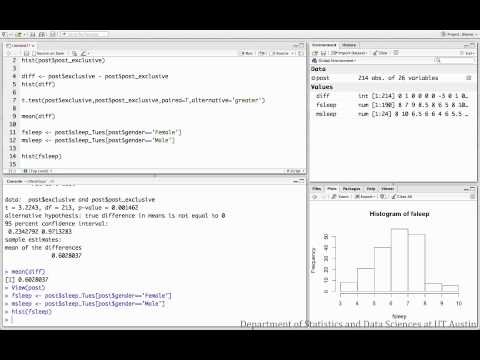

Conclusione del campione: Con t(df=27)=-0,42, p>0,05, non abbiamo trovato alcuna prova che suggerisca che gli studenti maschi e femmine dormano in modo diverso, in media, il martedì sera.