Espansioni Binomiali con il Triangolo di Pascal
Considera le seguenti potenze espanse di (a + b)n, dove a + b è un binomio qualsiasi e n è un numero intero. Cerca dei modelli.
Ogni espansione è un polinomio. Ci sono alcuni modelli da notare.
1. C’è un termine in più della potenza dell’esponente, n. Cioè, ci sono termini nell’espansione di (a + b)n.
2. In ogni termine, la somma degli esponenti è n, la potenza a cui è elevato il binomio.
3. Gli esponenti di a cominciano con n, la potenza del binomio, e diminuiscono fino a 0. L’ultimo termine non ha alcun fattore di a. Il primo termine non ha alcun fattore di b, quindi le potenze di b iniziano con 0 e aumentano fino a n.
4. I coefficienti iniziano da 1 e aumentano attraverso certi valori circa “a metà” e poi diminuiscono attraverso questi stessi valori fino a 1.
Esploriamo ulteriormente i coefficienti. Supponiamo di voler trovare un’espansione di (a + b)6. I modelli che abbiamo appena notato indicano che ci sono 7 termini nell’espansione:
a6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6.
Come possiamo determinare il valore di ogni coefficiente, ci? Possiamo farlo in due modi. Il primo metodo consiste nello scrivere i coefficienti in una matrice triangolare, come segue. Questo è noto come triangolo di Pascal: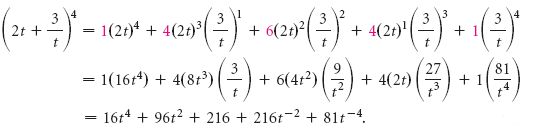
Ci sono molti modelli nel triangolo. Trovane quanti più puoi.
Forse hai scoperto un modo per scrivere la prossima riga di numeri, dati i numeri della riga precedente. Ci sono sempre degli 1 all’esterno. Ogni numero rimanente è la somma dei due numeri sopra di esso. Proviamo a trovare un’espansione per (a + b)6 aggiungendo un’altra riga usando i modelli che abbiamo scoperto:
Vediamo che nell’ultima riga
il primo e l’ultimo numero sono 1;
il secondo numero è 1 + 5, o 6;
il terzo numero è 5 + 10, o 15;
il quarto numero è 10 + 10, o 20;
il quinto numero è 10 + 5, o 15; e
il sesto numero è 5 + 1, o 6.
Quindi l’espansione per (a + b)6 è
(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Per trovare un’espansione di (a + b)8, completiamo altre due righe del triangolo di Pascal: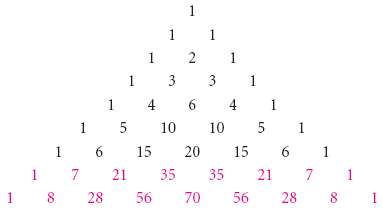
Quindi l’espansione di è
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Possiamo generalizzare i nostri risultati come segue.
Il teorema del binomio usando il triangolo di Pascal
Per qualsiasi binomio a + b e qualsiasi numero naturale n,
(a + b)n = c0anb0 + c1an-1b1 + c2an-2b2 + …. + cn-1a1bn-1 + cna0bn,
dove i numeri c0, c1, c2,…., cn-1, cn sono della (n + 1)-sima riga del triangolo di Pascal.
Esempio 1 Espandi: (u – v)5.
Soluzione Abbiamo (a + b)n, dove a = u, b = -v, e n = 5. Usiamo la sesta riga del triangolo di Pascal:
1 5 10 10 5 1
Allora abbiamo
(u – v)5 = 5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5.
Nota che i segni dei termini si alternano tra + e -. Quando la potenza di -v è dispari, il segno è -.
Esempio 2 Espandi: (2t + 3/t)4.
Soluzione Abbiamo (a + b)n, dove a = 2t, b = 3/t, e n = 4. Usiamo la quinta riga del triangolo di Pascal:
1 4 6 4 1
Allora abbiamo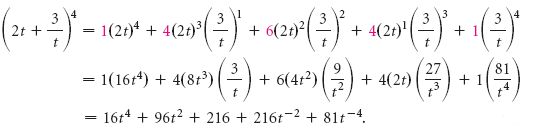
Espansione binomiale usando la notazione fattoriale
Supponiamo di voler trovare l’espansione di (a + b)11. Lo svantaggio di usare il triangolo di Pascal è che dobbiamo calcolare tutte le righe precedenti del triangolo per ottenere la riga necessaria per l’espansione. Il metodo seguente evita questo. Ci permette anche di trovare un termine specifico – ad esempio, l’ottavo termine – senza calcolare tutti gli altri termini dell’espansione. Questo metodo è utile in corsi come matematica finita, calcolo e statistica, e usa la notazione dei coefficienti binomiali 
.
Il teorema binomiale usando la notazione fattoriale
Per qualsiasi binomio (a + b) e qualsiasi numero naturale n,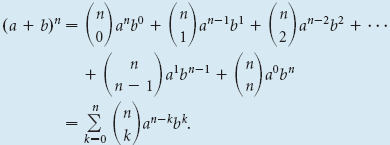
.
Il teorema binomiale può essere dimostrato per induzione matematica. (Vedi Esercizio 63.) Questa forma mostra perché è chiamato coefficiente binomiale.
Esempio 3 Espandi: (x2 – 2y)5.
Soluzione Abbiamo (a + b)n, dove a = x2, b = -2y, e n = 5. Quindi, usando il teorema binomiale, abbiamo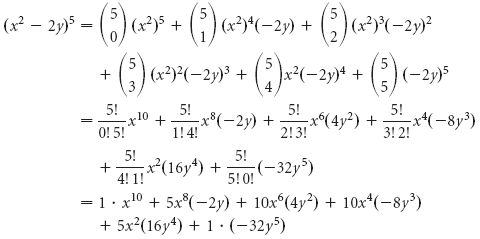
Infine (x2 – 2y)5 = x10 – 10x8y + 40x6y2 – 80x4y3 + 80x2y4 – 32y5.
Esempio 4 Espandi: (2/x + 3√x)4.
Soluzione Abbiamo (a + b)n, dove a = 2/x, b = 3√x, e n = 4. Quindi, usando il teorema binomiale, abbiamo
Infine (2/x + 3√x)4 = 16/x4 + 96/x5/2 + 216/x + 216×1/2 + 81×2.
Trovare un termine specifico
Supponiamo di voler determinare solo un termine particolare di una espansione. Il metodo che abbiamo sviluppato ci permetterà di trovare tale termine senza calcolare tutte le righe del triangolo di Pascal o tutti i coefficienti precedenti.
Nota che nel teorema binomiale, 
ci dà il 1° termine, 
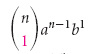ci dà il 2° termine, 
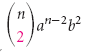ci dà il 3° termine, e così via. Questo può essere generalizzato come segue.
Trovare il (k + 1)-st termine
Il (k + 1)-st termine di (a + b)n è 
.
Esempio 5 Trovare il 5° termine nell’espansione di (2x – 5y)6.
Soluzione Innanzitutto, notiamo che 5 = 4 + 1. Quindi, k = 4, a = 2x, b = -5y, e n = 6. Allora il 5° termine dell’espansione è
Esempio 6 Trova l’8° termine nell’espansione di (3x – 2)10.
Soluzione Innanzitutto, notiamo che 8 = 7 + 1. Quindi, k = 7, a = 3x, b = -2, e n = 10. Allora l’ottavo termine dell’espansione è
Numero totale di sottoinsiemi
Supponiamo che un insieme abbia n oggetti. Il numero di sottoinsiemi contenenti k elementi . Il numero totale di sottoinsiemi di un insieme è il numero di sottoinsiemi con 0 elementi, più il numero di sottoinsiemi con 1 elemento, più il numero di sottoinsiemi con 2 elementi, e così via. Il numero totale di sottoinsiemi di un insieme con n elementi è
.
Ora consideriamo l’espansione di (1 + 1)n:
.
Quindi il numero totale di sottoinsiemi è (1 + 1)n, ovvero 2n. Abbiamo dimostrato quanto segue.
Numero totale di sottoinsiemi
Il numero totale di sottoinsiemi di un insieme con n elementi è 2n.
Esempio 7 L’insieme {A, B, C, D, E} quanti sottoinsiemi ha?
Soluzione L’insieme ha 5 elementi, quindi il numero di sottoinsiemi è 25, ovvero 32.
Esempio 8 Wendy’s, una catena nazionale di ristoranti, offre i seguenti condimenti per i suoi hamburger:
{catsup, senape, maionese, pomodoro, lattuga, cipolle, sottaceti, condimento, formaggio}.
Quanti tipi diversi di hamburger può servire Wendy’s, escludendo la dimensione dell’hamburger o il numero di polpette?
Soluzione I condimenti di ogni hamburger sono gli elementi di un sottoinsieme dell’insieme di tutti i condimenti possibili, l’insieme vuoto è un semplice hamburger. Il numero totale di possibili hamburger è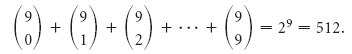
Quindi Wendy’s serve gli hamburger in 512 modi diversi.