La distribuzione normale standard può essere utile anche per calcolare i percentili
. Per esempio, la mediana è il 50° percentile, il primo quartile è il 25° percentile e il terzo quartile è il 75° percentile. In alcuni casi può essere interessante calcolare altri percentili, per esempio il 5° o il 95°. La formula seguente è usata per calcolare i percentili di una distribuzione normale.
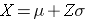
dove μ è la media e σ è la deviazione standard della variabile X, e Z è il valore della distribuzione normale standard per il percentile desiderato.
Esempio:
- L’IMC medio per gli uomini di 60 anni è 29 con una deviazione standard di 6.
- L’IMC medio per le donne di 60 anni è 28 con una deviazione standard di 7.
Qual è il 90° percentile dell’IMC per gli uomini?
Il 90° percentile è l’IMC che contiene il 90% degli IMC sotto di esso e il 10% sopra di esso, come illustrato nella figura sottostante.
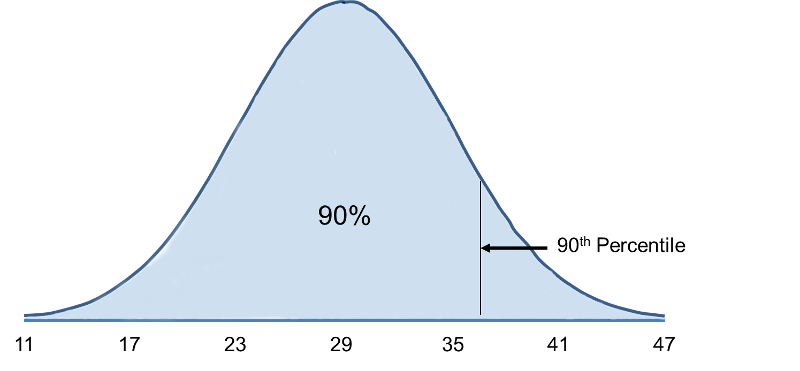
Per calcolare il 90° percentile, usiamo la formula X=μ + Zσ, e useremo la tabella standard della distribuzione normale, tranne che lavoreremo in direzione opposta. In precedenza siamo partiti da una particolare “X” e abbiamo usato la tabella per trovare la probabilità. Tuttavia, in questo caso vogliamo iniziare con una probabilità del 90% e trovare il valore di “X” che la rappresenta.
Così cominciamo andando all’interno della tabella di distribuzione normale standard per trovare l’area sotto la curva più vicina a 0,90, e da questo possiamo determinare il corrispondente punteggio Z. Una volta che abbiamo questo possiamo usare l’equazione X=μ + Zσ, perché sappiamo già che la media e la deviazione standard sono 29 e 6, rispettivamente.
Quando andiamo nella tabella, troviamo che il valore 0,90 non è esattamente lì, tuttavia, i valori 0,8997 e 0,9015 sono lì e corrispondono a valori Z di 1,28 e 1,29, rispettivamente (cioè, l’89,97% dell’area sotto la curva normale standard è sotto 1,28). Il valore Z esatto che tiene il 90% dei valori al di sotto di esso è 1,282 che è stato determinato da una tabella di probabilità normale standard con più precisione.
Utilizzando Z=1,282 il 90° percentile di BMI per gli uomini è: X = 29 + 1,282(6) = 36,69.
Interpretazione: Il novanta per cento dell’IMC negli uomini di 60 anni è inferiore a 36,69. Il dieci per cento degli IMC negli uomini di 60 anni sono superiori a 36,69.
Qual è il 90° percentile dell’IMC tra le donne di 60 anni? Ricordiamo che l’IMC medio per le donne di 60 anni è 28 con una deviazione standard di 7.
Risposta
La tabella sottostante mostra i valori Z per i percentili comunemente usati.
|
Percentile |
Z |
|
|---|---|---|
|
1° |
-2.326 |
|
|
2.5° |
-1.960 |
|
|
5° |
-1.645 |
|
|
10° |
-1.282 |
|
|
25° |
-0.675 |
|
|
50° |
0 |
|
|
75° |
0.675 |
|
|
90° |
1.282 |
|
|
95° |
1.645 |
|
|
97.5° |
1.960 |
|
|
99° |
2.326 |
I percentili di altezza e peso sono usati dai pediatri per valutare lo sviluppo rispetto ai bambini dello stesso sesso ed età. Per esempio, se il peso di un bambino per l’età è estremamente basso, potrebbe essere un’indicazione di malnutrizione. I grafici di crescita sono disponibili su http://www.cdc.gov/growthcharts/.
Per le bambine, la lunghezza media del corpo a 10 mesi è 72 centimetri con una deviazione standard di 3 centimetri. Supponiamo che una bambina di 10 mesi abbia una lunghezza misurata di 67 centimetri. Come si confronta la sua lunghezza con quella di altre bambine di 10 mesi?
Risposta
Un emocromo completo (CBC) è un test comunemente eseguito. Un componente dell’emocromo è il conteggio dei globuli bianchi (WBC), che può essere indicativo di infezione se il conteggio è alto. La conta dei globuli bianchi è approssimativamente distribuita normalmente nelle persone sane con una media di 7550 globuli bianchi per mm3 (cioè, per microlitro) e una deviazione standard di 1085. Quale proporzione di soggetti ha una conta di WBC superiore a 9000?
Risposta