Ritorna all’indice delle lezioni | Fai le lezioni in ordine | Pagina facile da stampare
Funzioni esponenziali: Interesse composto (pagina 4 di 5)
Sezioni: Introduzione, Valutazione, Grafico, Interesse composto, L’esponenziale naturale
Una equazione esponenziale molto importante è la formula dell’interesse composto:
![]()
…dove “A” è l’importo finale, “P” è l’importo iniziale (o “capitale”), “r” è il tasso di interesse (espresso in decimale), “n” è il numero di maggiorazioni all’anno, e “t” è il numero totale di anni.
Per quanto riguarda le variabili, n si riferisce al numero di maggiorazioni in un anno, non al numero totale di maggiorazioni durante la vita dell’investimento. Se l’interesse è composto annualmente, allora n = 1; se semestrale, allora n = 2; trimestrale, allora n = 4; mensile, allora n = 12; settimanale, allora n = 52; giornaliero, allora n = 365; e così via, indipendentemente dal numero di anni coinvolti. Inoltre, “t” deve essere espresso in anni, perché i tassi di interesse sono espressi in questo modo. Se un esercizio afferma che il capitale è stato investito per sei mesi, è necessario convertirlo in 6/12 = 0,5 anni; se è stato investito per 15 mesi, allora t = 15/12 = 1,25 anni; se è stato investito per 90 giorni, allora t = 90/365 di un anno; e così via.
Nota che, per qualsiasi tasso di interesse dato, la formula di cui sopra si semplifica nella semplice forma esponenziale alla quale siamo abituati. Per esempio, lasciamo che il tasso d’interesse r sia del 3%, composto mensilmente, e che l’importo dell’investimento iniziale sia di 1250 dollari. Allora l’equazione dell’interesse composto, per un periodo di investimento di t anni, diventa:
![]()
…dove la base è 1.0025 e l’esponente è l’espressione lineare 12t.
Per fare problemi di parole di interesse composto, generalmente l’unica parte difficile è capire quali valori vanno dove nella formula di interesse composto. Una volta che hai inserito correttamente tutti i valori, puoi risolvere per qualsiasi variabile rimanga.
Advertisement
- Supponiamo che abbiate bisogno di 10.000 dollari tra trentasei mesi, quando vostro figlio inizierà l’università. Vuoi investire in uno strumento che renda il 3,5% di interesse, composto mensilmente. Quanto dovresti investire?
Per risolvere questo, devo capire quali valori vanno con quali variabili. In questo caso, voglio finire con 10.000 dollari, quindi A = 10.000. Il tasso d’interesse è del 3,5%, quindi, espresso come decimale, r = 0,035. Il periodo di tempo è di trentasei mesi, quindi t = 36/12 = 3. E l’interesse è composto mensilmente, quindi n = 12. L’unica variabile rimanente è P, che sta per quanto ho iniziato. Dal momento che sto cercando di capire quanto investire in primo luogo, allora risolvere per P ha senso. Inserirò tutti i valori noti, e poi risolverò la variabile rimanente:
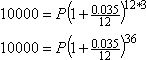
La tentazione a questo punto è di semplificare sul lato destro, e poi dividere per risolvere P. Non farlo; tende all’errore di arrotondamento, e può metterti nei guai più tardi. Invece, rimanete esatti, e fate prima la divisione simbolicamente (ed esattamente):
![]()
Ora farò l’intera semplificazione nella mia calcolatrice, lavorando dall’interno all’esterno, così tutto viene portato in memoria e ottengo una risposta più esatta possibile:

Ho bisogno di investire circa 9004 dollari.62.
(Il problema non specificava come arrotondare, ma in questo caso non ne aveva bisogno. I problemi in dollari e centesimi arrotondano sempre a due cifre decimali). Copyright © Elizabeth Stapel 2002-2011 Tutti i diritti riservati
Si dovrebbe memorizzare la formula dell’interesse composto, ma si dovrebbe anche memorizzare il significato di ciascuna delle variabili nella formula. Anche se vi sarà data la formula nel test, è improbabile che vi sarà dato il significato delle variabili e, senza il significato, non sarete in grado di completare gli esercizi.
<< Previous Top | 1 | 2 | 3 | 4 | 5 | Return to Index Next >>
|
Cita questo articolo come: |
Stapel, Elizabeth. “Funzioni esponenziali: Interesse composto”. Purplemath. Disponibile da 2016
|