Obiettivi di apprendimento
- Per definire l’emivita.
- Determinare la quantità di sostanza radioattiva che rimane dopo un dato numero di emivite.
Se un dato isotopo è radioattivo o meno è una caratteristica di quel particolare isotopo. Alcuni isotopi sono stabili all’infinito, mentre altri sono radioattivi e decadono attraverso una caratteristica forma di emissione. Col passare del tempo, sempre meno dell’isotopo radioattivo sarà presente, e il livello di radioattività diminuisce. Un aspetto interessante e utile del decadimento radioattivo è l’emivita. L’emivita di un isotopo radioattivo è la quantità di tempo che impiega la metà dell’isotopo radioattivo a decadere. L’emivita di uno specifico isotopo radioattivo è costante; non è influenzata dalle condizioni ed è indipendente dalla quantità iniziale di quell’isotopo.
Considera il seguente esempio. Supponiamo di avere 100,0 g di 3H (trizio, un isotopo radioattivo dell’idrogeno). Ha un tempo di dimezzamento di 12,3 anni. Dopo 12,3 anni, metà del campione sarà decaduto in 3He emettendo una particella beta, così che rimangono solo 50,0 g del 3H originale. Dopo altri 12,3 anni – per un totale di 24,6 anni – un’altra metà del 3H rimanente sarà decaduta, lasciando 25,0 g di 3H. Dopo altri 12,3 anni – ora un totale di 36,9 anni – un’altra metà del 3H rimanente sarà decaduta, lasciando 12,5 g di 3H. Questa sequenza di eventi è illustrata nella Figura \(\PageIndex{1}}).
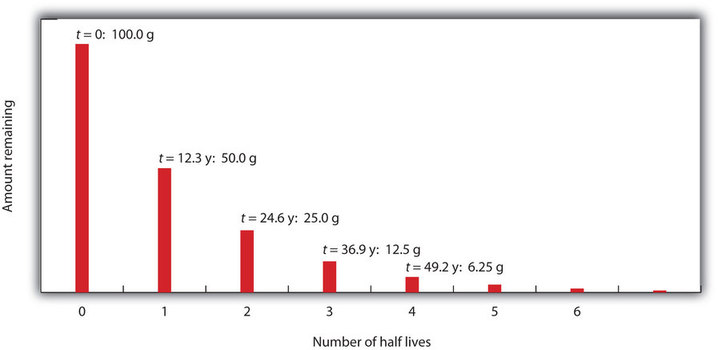
Possiamo determinare la quantità di un isotopo radioattivo che rimane dopo un dato numero di emivite usando la seguente espressione:
\
dove n è il numero di emivite. Questa espressione funziona anche se il numero di emivite non è un numero intero.
Esempio \(\PageIndex{1}\): Fluoro-20
L’emivita di 20F è 11,0 s. Se un campione contiene inizialmente 5,00 g di 20F, quanto 20F rimane dopo 44,0 s?
Soluzione
Se confrontiamo il tempo che è passato con l’emivita dell’isotopo, notiamo che 44,0 s sono esattamente 4 emivite, quindi possiamo usare l’equazione \ref{E1} con \(n = 4\). Sostituendo e risolvendo si ottiene quanto segue:
&=5.00\: g \times \dfrac{1}{16} &=0.313\: g \fine{align*}]
Meno di un terzo di un grammo di 20F rimane.
Esercizio \(\PageIndex{1}): Titanio-44
L’emivita del 44Ti è di 60,0 anni. Un campione contiene inizialmente 0,600 g di 44Ti. Quanto 44Ti rimane dopo 180,0 anni?
Risposta
0,075 g.
Le mezze vite degli isotopi vanno da frazioni di microsecondo a miliardi di anni. La tabella \(\PageIndex{1}) elenca le emivite di alcuni isotopi.
| Isotopo | Half-Vita |
|---|---|
| 3H | 12.3 y |
| 14C | 5.730 y |
| 40K | 1.26 × 109 y |
| 51Cr | 27.70 d |
| 90Sr | 29.1 y |
| 131I | 8.04 d |
| 222Rn | 3.823 d |
| 235U | 7.04 × 108 y |
| 238U | 4.47 × 109 y |
| 241Am | 432,7 y |
| 248Bk | 23.7 h |
| 260Sg | 4 ms |
Esempio \(\PageIndex{2}\): Iodio-125
L’isotopo \(\ce{I})-125 è usato in certe procedure di laboratorio e ha un’emivita di 59,4 giorni. Se l’attività iniziale di un campione di \(\ce{I})-125 è \(32.000 \: \), quanta attività sarà presente in 178,2 giorni?
Soluzione
Iniziamo a determinare quante emivite sono rappresentate da 178.2 giorni:
Poi contiamo semplicemente l’attività:
Assicurati di tenere a mente che il conteggio iniziale è al tempo zero \(\sinistra( t_0 \destra)\) e sottraiamo da quel conteggio la prima emivita. La seconda emivita ha un’attività pari alla metà del conteggio precedente (non il conteggio iniziale).
L’equazione \(\ref{Eq1}) può essere usata per calcolare la quantità di radioattività rimanente dopo un dato tempo:
dove \(N_t =\) attività al tempo \(t\) e \(N_0 =\) attività iniziale al tempo \(t = 0\).
Se abbiamo un’attività iniziale di \(42.000 \: \text{cpm}\), quale sarà l’attività dopo quattro emivite?
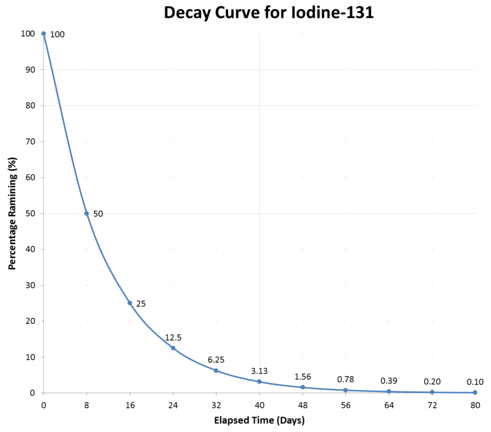
Curva tipica di decadimento radioattivo.
Il grafico sopra illustra una tipica curva di decadimento per \(\ce{I}-125\). L’attività diminuisce di metà durante ogni emivita successiva.
Esercizio \(\PageIndex{2})
Un campione di \(\ce{Ac})-225 conteneva originariamente 80 grammi e dopo 50 giorni rimangono solo 2,5 grammi dell’originale \(\ce{Ac})-225. Qual è l’emivita di \(\ce{Ac})-225?
Risposta
10 giorni
Guardando più da vicino: emivita degli elementi radioattivi
Molte persone pensano che l’emivita di un elemento radioattivo rappresenti la quantità di tempo in cui un elemento è radioattivo. In realtà, è il tempo necessario a metà, e non a tutto, l’elemento per decadere radioattivamente. Occasionalmente, tuttavia, l’elemento figlio è anch’esso radioattivo, quindi bisogna considerare anche la sua radioattività.
La vita lavorativa prevista di un rilevatore di fumo a ionizzazione (descritto nel saggio di apertura) è di circa 10 anni. In questo tempo, l’americio-241, che ha un’emivita di circa 432 anni, perde meno del 4% della sua radioattività. Un’emivita di 432 anni può sembrarci lunga, ma non è molto lunga come emivita. L’uranio-238, l’isotopo più comune dell’uranio, ha un’emivita di circa 4,5 × 109 anni, mentre il torio-232 ha un’emivita di 14 × 109 anni. L’isotopo più longevo del laurenzio, 262Lr, ha un’emivita di 3,6 ore, mentre l’isotopo più corto del laurenzio, 252Lr, ha un’emivita di 0,36 s. Al momento in cui scriviamo, il più grande atomo mai rilevato ha numero atomico 118, numero di massa 293 e un’emivita di 120 ns. Riesci a immaginare quanto velocemente si debba fare un esperimento per determinare le proprietà di elementi che esistono per un tempo così breve?
Punti chiave
- I processi radioattivi naturali sono caratterizzati da un’emivita, il tempo che impiega la metà del materiale a decadere radioattivamente.
- La quantità di materiale rimasto dopo un certo numero di emivite può essere facilmente calcolata.
Esercizi di ripasso dei concetti
- Definire l’emivita.
- Descrivere un modo per determinare la quantità di isotopo radioattivo che rimane dopo un dato numero di emivite.
Risposte
- L’emivita è la quantità di tempo necessaria affinché la metà di un materiale radioattivo decada.
- Prendi la metà della quantità iniziale per ogni emivita di tempo trascorsa