La storia della fondazione di Microsoft è uno degli episodi più famosi della storia dell’informatica. Nel 1975, Paul Allen volò ad Albuquerque per dimostrare l’interprete BASIC che lui e Bill Gates avevano scritto per l’Altairmicrocomputer. Poiché nessuno di loro aveva un Altair funzionante, Allen e Gates testarono il loro interprete usando un emulatore che scrissero e che funzionava sul sistema informatico di Harvard. L’emulatore era basato su nient’altro che le specifiche pubblicate per il processore Intel 8080. Quando Allen finalmente fece girare il loro interprete su un vero Altair – di fronte alla persona che lui e Gates speravano avrebbe comprato il loro software – non aveva idea se avrebbe funzionato. Ma funzionò. Il mese successivo, Allen e Gates fondarono ufficialmente la loro nuova compagnia.
Oltre un secolo prima che Allen e Gates scrivessero il loro interprete BASIC, AdaLovelace scrisse e pubblicò un programma per computer. Anche lei scrisse un programma per un computer che le era stato solo descritto. Ma il suo programma, a differenza dell’interprete BASIC di Microsoft, non fu mai eseguito, perché il computer a cui mirava non fu mai costruito.
Il programma diLovelace è spesso chiamato il primo programma per computer del mondo. Non tutti sono d’accordo sul fatto che debba essere chiamato così. L’eredità di Lovelace, a quanto pare, è uno degli argomenti più discussi della storia dell’informatica. Walter Isaacson ha scritto che la disputa sulla portata e il merito dei suoi contributi costituisce una “specialità accademica minore”.1 Inevitabilmente, il fatto che Lovelace fosse una donna ha reso questa disputa molto accesa. Gli storici hanno citato tutti i tipi di prove primarie per sostenere che il credito dato a Lovelace è appropriato o immeritato. Ma sembrano spendere meno tempo a spiegare i dettagli tecnici della sua scrittura pubblicata, il che è un peccato, perché i dettagli tecnici sono la parte più affascinante della storia. Chi non vorrebbe sapere esattamente come dovrebbe funzionare un programma scritto nel 1843?
In tutta onestà, il programma della Lovelace non è facile da spiegare ai profani senza qualche sventolio di mano. Sono le complessità del suo programma, però, a renderlo doloroso. Sia che debba essere conosciuta o meno come “la prima programmatrice”, il suo programma era specificato con un grado di rigore che superava di gran lunga tutto ciò che veniva prima. Pensò attentamente a come le operazioni potevano essere organizzate in gruppi che potevano essere ripetuti, inventando così il ciclo. Si rese conto di quanto fosse importante tracciare lo stato delle variabili mentre cambiavano, introducendo un’annotazione per illustrare questi cambiamenti. Essendo io stesso un programmatore, sono sorpreso di vedere quanto di ciò che Lovelace stava facendo assomigli all’esperienza di scrivere software oggi.
Diamo quindi un’occhiata più da vicino al programma di Lovelace. Lo ha progettato per calcolare i numeri di Bernoulli. Per capire cosa sono, dobbiamo tornare indietro di un paio di millenni alla genesi di uno dei problemi più antichi della matematica.
Somma delle potenze
I Pitagorici vivevano sulle rive del Mediterraneo e adoravano i numeri. Uno dei loro passatempi era fare triangoli con i sassolini.

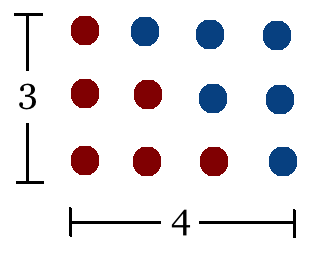
Un sassolino seguito da una fila di due sassolini fa un triangolo con tre sassolini. Aggiungete un’altra fila di tre sassolini e otterrete un triangolo contenente sei sassolini. Puoi continuare così, aggiungendo ogni volta una riga con un sassolino in più rispetto alla riga precedente. Un triangolo con sei file contiene 21 sassolini. Ma quanti sassolini contiene un triangolo con 423 righe?
Quello che i pitagorici cercavano era un modo per calcolare quanto segue senza fare tutte le addizioni:
Hanno capito che, se si mettono due triangoli della stessa dimensione uno contro l’altro in modo da formare un rettangolo, si può trovare l’area del triangolo e dividere per due per ottenere il numero di sassolini in ciascuno dei triangoli:
Archimede esplorò in seguito un problema simile. Era interessato alla seguente serie:
Si può visualizzare questa serie immaginando una pila di quadrati progressivamente più grandi (fatti di piccoli cubi), uno sopra l’altro, che formano una piramide.Archimede voleva sapere se c’era un modo semplice per dire quanti cubi sarebbero stati necessari per costruire una piramide con, diciamo, 423 livelli. Registrò una soluzione che permette anche un’interpretazione geometrica.2
Tre piramidi possono essere incastrate insieme per formare un prisma rettangolare con una piccola estrusione alta un cubo a un’estremità. Quella piccola estrusione è un atriangolo che obbedisce alle stesse regole che i pitagorici usavano per fare i loro triangoli di sassi. (Questo video potrebbe essere una spiegazione più utile di ciò che intendo.) Quindi il volume della forma intera è dato dalla seguente equazione:
Sostituendo l’equazione pitagorica per la somma dei primi nove numeri e facendo un po’ di algebra, si ottiene questo:Nel 499, il matematico e astronomo indiano Aryabhata pubblicò un’opera nota come Aryabhatiya, che includeva una formula per calcolare la somma dei cubi:
Una formula per la somma dei primi n numeri interi positivi elevati alla quarta potenza non fu pubblicata per altri 500 anni.3
A questo punto ci si potrebbe chiedere se esiste un metodo generale per trovare la somma dei primi n numeri interi elevati alla kesima potenza. Johann Faulhaber, un matematico tedesco e numerologo un po’ stravagante, fu in grado di calcolare formule per somme di numeri interi fino alla 17a potenza, che pubblicò nel 1631. Ma questo potrebbe avergli richiesto anni e non ha dichiarato una soluzione generale.4 Blaise Pascalfinalmente delineò un metodo generale nel 1665, sebbene dipendesse dal sapere prima come calcolare la somma di numeri interi elevati a ogni potenza minore.5 Per calcolare la somma dei primi n numeri interi positivi elevati alla sesta potenza, per esempio, bisognava prima sapere come calcolare la somma dei primi n numeri interi positivi elevati alla quinta potenza.
Una soluzione generale più pratica fu indicata nell’opera pubblicata postuma del matematico svizzero Jakob Bernoulli, morto nel 1705. Bernoulli iniziò a ricavare le formule per calcolare le somme dei primi n numeri interi positivi alla prima, seconda e terza potenza.6 Queste formule furono date in forma polinomiale, in modo da assomigliare alla seguente:
Utilizzando il triangolo di Pascal, Bernoulli si rese conto che questi polinomi seguivano uno schema prevedibile. Essenzialmente, Bernoulli ruppe i coefficienti di ogni termine in due fattori, uno dei quali poteva determinare usando il Triangolo di Pascal e l’altro che poteva derivare dall’interessante proprietà che tutti i coefficienti del polinomio sembravano sempre sommarsi a uno. Trovare l’esponente che dovrebbe essere attaccato ad ogni termine non era un problema, perché anche questo seguiva un modello prevedibile. Il fattore di ogni coefficiente che doveva essere calcolato usando la regola della somma a uno formava una sequenza che divenne nota come i numeri di Bernoulli.
La scoperta di Bernoulli non significava che fosse ora banale calcolare la somma dei primi n interi positivi a qualsiasi potenza. Per calcolare la somma dei primi n numeri interi positivi elevati alla kesima potenza, bisognava conoscere ogni numero di Bernoulli fino al kesimo numero di Bernoulli. Ogni numero di Bernoulli potrebbe essere calcolato solo se i numeri di Bernoulli precedenti fossero noti. Ma calcolare una lunga serie di numeri di Bernoulli era significativamente più facile che ricavare ogni formula di somma di potenze, quindi la scoperta di Bernoulli fu un grande progresso per la matematica.
Babbage
Charles Babbage nacque nel 1791, quasi un secolo dopo la morte di Bernoulli. Ho sempre avuto una vaga idea che Babbage avesse progettato ma non costruito un computer meccanico. Ma non ho mai capito del tutto come doveva funzionare quel computer. Le idee di base, guarda caso, non sono così difficili da capire, il che è una buona notizia. Il programma di Lovelace era progettato per essere eseguito su una delle macchine di Babbage, quindi dobbiamo fare un’altra veloce deviazione per parlare di come funzionavano quelle macchine.
Babbage progettò due distinte macchine di calcolo meccanico. La sua prima macchina si chiamava Difference Engine. Prima dell’invenzione della calcolatrice tascabile, la gente si affidava alle tavole logaritmiche per calcolare il prodotto di grandi numeri. Le grandi tabelle logaritmiche non sono difficili da creare, almeno concettualmente, ma il gran numero di calcoli che devono essere fatti per crearle significava che al tempo di Babbage spesso contenevano errori. Babbage, frustrato da questo, cercò di creare una macchina che potesse tabulare i logaritmi meccanicamente e quindi senza errori.7
La Difference Engine non era un computer, perché tutto quello che faceva era aggiungere e sottrarre. Sfruttava un metodo ideato dal matematico francese Gaspard de Prony che rompeva il processo di tabulazione dei logaritmi in piccoli passi.8 Questi piccoli passi implicavano solo addizione e sottrazione, il che significava che un piccolo esercito di persone senza alcuna speciale attitudine o formazione matematica poteva essere impiegato per produrre una tabella. Il metodo di De Prony, conosciuto come il metodo delle differenze divise, poteva essere usato per tabulare qualsiasi polinomio. I polinomi, a loro volta, potevano essere usati per approssimare funzioni logaritmiche e trigonometriche.
Per avere un’idea di come funzionava questo processo, si consideri la seguente semplice funzione polinomiale:
Il metodo delle differenze divise consiste nel trovare la differenza tra ogni valore successivo di y per diversi valori di x. Vengono poi trovate le differenze tra queste differenze, ed eventualmente le differenze tra queste stesse differenze successive, finché non appare una differenza costante. Le differenze possono poi essere usate per ottenere il prossimo valore del polinomio semplicemente aggiungendo.
Perché il polinomio di cui sopra è solo un polinomio di secondo grado, siamo in grado di trovare la differenza costante dopo solo due colonne di differenze:
| x | y | Diff 1 | Diff 2 |
|---|---|---|---|
| 1 | 2 | ||
| 2 | 5 | 3 | |
| 3 | 10 | 5 | 2 |
| 4 | 17 | 7 | 2 |
| 5 | ? | ? | 2 |
| … | … | … | … |
Ora, poiché sappiamo che la differenza costante è 2, possiamo trovare il valore diy quando x è 5 solo attraverso l’addizione. Se aggiungiamo 2 a 7, l’ultima voce della colonna “Diff 1”, otteniamo 9. Se aggiungiamo 9 a 17, l’ultima voce nella colonna y, otteniamo 26, la nostra risposta.
Il motore a differenza di Babbage aveva, per ogni colonna di differenza in una tabella come quella sopra, una colonna fisica di ingranaggi. Ogni ingranaggio era una cifra decimale e un’intera colonna era un numero decimale. Il Difference Engine aveva otto colonne di ingranaggi, così poteva tabulare un polinomio fino al settimo grado. Le colonne erano inizialmente impostate con valori corrispondenti ad una prima riga della tabella della differenza, elaborata in anticipo. Un operatore umano avrebbe poi girato un albero a manovella, facendo propagare la differenza costante attraverso la macchina man mano che i valori inseriti in ogni colonna venivano aggiunti alla successiva.
Babbage fu in grado di costruire una piccola sezione del motore a differenza e di usarlo per dimostrare le sue idee alle feste.9 Ma anche dopo aver speso una quantità di denaro pubblico pari al costo di due grandi navi da guerra, non costruì mai l’intera macchina.10 Babbage non poteva trovare nessuno all’inizio del 1800 che potesse fare il numero di ingranaggi di cui aveva bisogno con sufficiente precisione. Una DifferenceEngine funzionante non sarebbe stata costruita fino agli anni ’90, dopo l’avvento della lavorazione di precisione. C’è un grande video su YouTube che mostra un motore a differenza funzionante in prestito al Computer History Museum di Mountain View, che vale la pena guardare anche solo per ascoltare i meravigliosi suoni che la macchina produce mentre funziona.
Babbage alla fine perse interesse nel motore a differenza quando si rese conto che si poteva costruire una macchina molto più potente e flessibile. Il suo motore analitico era la macchina che oggi conosciamo come il computer meccanico di Babbage. Il motore analitico era basato sulle stesse colonne di ingranaggi usate nel motore a differenza, ma mentre il motore a differenza aveva solo otto colonne, il motore analitico doveva averne molte centinaia in più. Il motore analitico poteva essere programmato usando schede perforate come un telaio Jacquard e poteva moltiplicare e dividere così come aggiungere e sottrarre. Per eseguire una di queste operazioni, una sezione della macchina chiamata “mulino” si riorganizzava nella configurazione appropriata, leggeva gli operandi da altre colonne usate per la memorizzazione dei dati, e poi scriveva il risultato in un’altra colonna.
Babbage chiamò la sua nuova macchina Motore Analitico perché era abbastanza potente da fare qualcosa di simile all’analisi matematica. Il motore a differenza poteva tabulare un polinomio, ma il motore analitico sarebbe stato in grado di calcolare, per esempio, i coefficienti dell’espansione polinomiale di un’altra espressione. Era una macchina straordinaria, ma il governo britannico saggiamente rifiutò di finanziarne la costruzione. Così Babbage andò all’estero, in Italia, per cercare di raccogliere supporto per la sua idea.
Note del traduttore
A Torino, Babbage incontrò l’ingegnere italiano e futuro primo ministro Luigi Menabrea. Convinse Menabrea a scrivere uno schema di ciò che l’AnalyticalEngine avrebbe potuto realizzare. Nel 1842, Menabrea pubblicò un documento sull’argomento in francese. L’anno seguente, Lovelace pubblicò una traduzione di Menabrea in inglese.
Lovelace, allora conosciuta come Ada Byron, incontrò per la prima volta Babbage ad una festa nel 1833, quando lei aveva 17 anni e lui 41.11 Lovelace era affascinata dal motore a differenza di Babbage. Poteva anche capire come funzionava, perché era stata ampiamente istruita in matematica durante la sua infanzia. Sua madre, Annabella Milbanke, aveva deciso che una solida base in matematica wouldward off il selvaggio, sensibilità romantica che possedeva Lovelace padre, LordByron, il famoso poeta. Dopo essersi incontrati nel 1833, Lovelace e Babbage rimasero parte dello stesso circolo sociale e si scrissero spesso.
Ada Byron sposò William King nel 1835. King divenne in seguito il conte di Lovelace, facendo di Ada la contessa di Lovelace. Anche dopo aver avuto tre figli, continuò la sua istruzione in matematica, impiegando Augustus de Morgan, che scoprì le leggi di De Morgan, come suo precettore.12 Lovelace vide immediatamente il potenziale della macchina analitica di Babbage e fu desiderosa di lavorare con lui per promuovere l’idea. Un amico le suggerì di tradurre l’articolo di Menabrea per un pubblico inglese.13
L’articolo di Menabrea dava una breve panoramica del funzionamento del motore a differenza, poi mostrava come il motore analitico sarebbe stato una macchina di gran lunga superiore. Il Motore Analitico sarebbe stato così potente da poter “formare il prodotto di due numeri, ciascuno contenente venti cifre, in tre minuti “14 (corsivo nell’originale). Menabrea diede ulteriori esempi delle capacità della macchina, dimostrando come potesse risolvere un semplice sistema di equazioni lineari ed espandere il prodotto di due espressioni binomiali. In entrambi i casi, Menabrea forniva quelli che Lovelace chiamava “diagrammi di sviluppo”, che elencavano questa sequenza di operazioni che avrebbero dovuto essere eseguite per calcolare la risposta corretta.15 Questi erano programmi nello stesso senso in cui il programma di Lovelace era un programma e furono originariamente pubblicati l’anno prima. Ma, come vedremo, i programmi di Menabrea erano solo semplici esempi di ciò che era possibile, ed erano tutti banali, nel senso che non richiedevano alcun tipo di ramificazione o looping.
Lovelace aggiunse una serie di note alla sua traduzione dell’articolo di Menabrea, che nel complesso erano molto più lunghe del lavoro originale. Fu qui che fece i suoi maggiori contributi all’informatica. Nella nota A, che Lovelace ha allegato alla descrizione iniziale di Menabrea del motore analitico, Lovelace ha spiegato a una certa lunghezza e spesso in un linguaggio lirico la promessa di una macchina che potrebbe eseguire operazioni matematiche arbitrarie. Prevedeva che una macchina come il Motore Analitico non si limitasse solo ai numeri e potesse in effetti agire su qualsiasi oggetto “le cui relazioni fondamentali reciproche potessero essere espresse da quelle della scienza astratta delle operazioni, e che fossero anche suscettibili di adattamenti all’azione della notazione operativa e del meccanismo del motore”.16 Aggiunse che la macchina avrebbe potuto un giorno, per esempio, comporre musica. Questa intuizione era tanto più notevole se si considera che Menabrea vedeva il Motore Analitico principalmente come uno strumento per automatizzare “il calcolo lungo e arido”, che avrebbe liberato le capacità intellettuali di brillanti scienziati per un pensiero più avanzato.17 La miracolosa lungimiranza che Lovelace dimostrò nella nota A è una delle ragioni principali per cui oggi è celebrata.
L’altra nota famosa è la nota G. Lovelace inizia la nota G sostenendo che, nonostante i suoi impressionanti poteri, non si può dire che la macchina analitica “pensi” davvero. Questa parte della nota G è ciò che Alan Turing avrebbe in seguito chiamato “Obiezione di Lady Lovelace”. Tuttavia, Lovelace continua, la macchina può doextraordinary cose. Per illustrare la sua capacità di gestire problemi ancora più complessi, Lovelace fornisce il suo programma che calcola i numeri di Bernoulli.
Il programma completo, nel formato “diagramma di sviluppo” espanso che Lovelace spiega nella nota D, può essere visto qui.Il programma è essenzialmente una lista di operazioni, specificate usando i simboli matematici usuali. Non sembra che Babbage o Lovelace siano arrivati a sviluppare qualcosa di simile a un insieme di codici operativi per il motore analitico.
Anche se Lovelace stava descrivendo un metodo per calcolare l’intera sequenza di numeri di Bernoulli fino a qualche limite, il programma che ha fornito illustrava solo un passo di quel processo. Il suo programma calcolò un numero che chiamò B7, che i matematici moderni conoscono come l’ottavo numero di Bernoulli. Il suo programma cercava quindi di risolvere la seguente equazione:
Nella precedente, ogni termine rappresenta un coefficiente nella formula polinomiale per la somma di numeri interi ad una particolare potenza. Qui la potenza è otto, poiché l’ottavo numero di Bernoulli appare per primo nella formula per la somma di numeri interi positivi all’ottava potenza. I numeri B e A rappresentano i due tipi di fattori che Bernoulli ha scoperto. Da B1 a B7 sono tutti diversi numeri di Bernoulli, indicizzati secondo l’indicizzazione di Lovelace. Da A0 a A5 rappresentano i fattori dei coefficienti che Bernoulli poteva calcolare usando il triangolo di Pascal. I valori di A0, A1, A3 e A5 appaiono sotto. Qui n rappresenta l’indice del numero di Bernoulli nella sequenza dei numeri dispari di Bernoulli a partire dal primo. Il programma di Lovelace usava n = 4.
Ho creato una traduzione del programma di Lovelace in C, che può essere più facile da seguire. Il programma di Lovelace calcola prima A0 e il prodotto B1A1. Poi entra in un ciclo che si ripete due volte per calcolare B3A3 e B5A5, poiché questi si formano secondo uno schema identico. Dopo che ogni prodotto è stato calcolato, viene aggiunto a tutti i prodotti precedenti, in modo che alla fine del programma sia stata ottenuta la somma completa.
Ovviamente la traduzione in C non è un’esatta ricreazione del programma di Lovelace.dichiara le variabili sullo stack, per esempio, mentre le variabili di Lovelace erano più simili ai registri. Ma rende evidenti le parti del programma di Lovelace che erano così preveggenti. Il programma C contiene due cicli while, uno annidato dentro l’altro. Il programma di Lovelace non aveva esattamente i cicli while, ma faceva gruppi di operazioni e nel testo della sua nota specificava quando dovevano ripetersi. La variabile v10, nel programma originale e nella traduzione in C, funziona come una variabile contatore che diminuisce ad ogni ciclo, un metodo che qualsiasi programmatore conosce bene. Infatti, a parte la profusione di variabili con nomi poco utili, la traduzione in C del programma di Lovelace non sembra affatto aliena.
L’altra cosa che vale la pena menzionare rapidamente è che tradurre il programma di Lovelace in C non è stato così difficile, grazie al dettaglio presente nel suo diagramma.A differenza delle tabelle di Menabrea, la sua tabella include una colonna etichettata “Indicazione di cambiamento nel valore di qualsiasi variabile”, che rende molto più facile seguire la mutazione di stato attraverso il programma. Aggiunge qui un indice in apice ad ogni variabile per indicare i valori successivi che essa contiene. Un apice di due, per esempio, significa che il valore usato qui è il secondo valore che è stato assegnato alla variabile dall’inizio del programma.
Il primo programmatore?
Dopo aver tradotto il programma di Lovelace in C, ho potuto eseguirlo sul mio computer. Con mia frustrazione, continuavo a ottenere il risultato sbagliato. Dopo un po’ di bugging, ho finalmente capito che il problema non era il codice che avevo scritto. Il bug era nell’originale!
Nel suo “diagramma di sviluppo”, Lovelace dà la quarta operazione comev5 / v4. Ma l’ordine corretto qui è v4 / v5. Questo potrebbe essere stato un errore di battitura e non un errore nel programma ideato da Lovelace. Tuttavia, questo deve essere il più vecchio bug dell’informatica. Mi sono meravigliato del fatto che, per circa dieci minuti, senza saperlo, ho lottato con questo primo bug in assoluto.
Jim Randall, un altro blogger che ha tradotto il programma di Lovelace in Python, ha notato questo bug di divisione e altri due problemi. Cosa dice di Ada Lovelace il fatto che il suo programma pubblicato contenga bug minori? Forse dimostra che stava cercando di scrivere non solo una dimostrazione ma un vero programma. Dopo tutto, si può davvero scrivere qualcosa di più di programmi giocattolo se non si scrivono anche molti bug?
Un articolo di Wikipedia chiama Lovelace la prima a pubblicare un “programma complesso”.18 Forse questo è il modo giusto di pensare a Lovelace. Menabrea pubblicò “diagrammi di sviluppo” nel suo articolo un anno prima che Lovelace pubblicasse la sua traduzione. Babbage scrisse anche più di venti programmi che non pubblicò mai.19 Quindi non è del tutto esatto dire che Lovelace scrisse o pubblicò il primo programma, anche se c’è sempre spazio per cavillare su cosa costituisca esattamente un “programma”. Anche così, il programma di Lovelace era molto più avanti di qualsiasi altra cosa che fosse stata pubblicata prima. Il programma più lungo che Menabrea presentò era lungo 11 operazioni e non conteneva né loop né rami; il programma di Lovelace contiene 25 operazioni e un loop annidato (e quindi una ramificazione). Menabrea scrisse quanto segue verso la fine del suo documento:
Quando una volta che il motore sarà stato costruito, la difficoltà si ridurrà alla realizzazione delle schede; ma poiché queste sono semplicemente la traduzione di formule algebriche, sarà facile affidarne l’esecuzione ad un operaio, per mezzo di qualche semplice notazione.20
Né Babbage né Menabrea erano particolarmente interessati ad applicare il Motore Analitico a problemi al di là delle immediate sfide matematiche che per prime avevano spinto Babbage a costruire macchine calcolatrici. Lovelace vide che il motore analitico era capace di molto più di quanto Babbage o Menabrea potessero immaginare. Lovelace capì anche che “il fare le carte” non sarebbe stato un semplice ripensamento e che poteva essere fatto bene o fatto male. Questo è difficile da apprezzare senza capire il suo programma dalla Nota G e vedere da soli la cura che ha messo nel progettarlo. Ma avendo fatto questo, potreste essere d’accordo che Lovelace, anche se non è stata la prima programmatrice, è stata la prima programmatrice a meritare questo titolo.
Se ti è piaciuto questo post, altri come questo escono ogni quattro settimane! Segui @TwoBitHistory su Twitter o iscriviti al feed RSS per essere sicuro di sapere quando esce un nuovo post.
Precedentemente su TwoBitHistory…
Il post di questa settimana: Parsing il prestigioso pedigree di Vim!https://t.co/1YUszI5dIC
– TwoBitHistory (@TwoBitHistory) August 5, 2018
-
Walter Isaacson, The Innovators (New York: Simon & Schuster Paperbacks, 2015), 25.
-
Janet Beery, “Somme di potenze di interi positivi: Archimede,” Mathematical Association of America, accessed August 18, 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-archimedes-287-212-bce-greece-italy.
-
Janet Beery, “Sums of Powers of Positive Integers: Abu Ali Al-Hasan Ibn Al-Hasan Ibn Al-Haytham”, Mathematical Association of America, accesso 18 agosto 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-abu-ali-al-hasan-ibn-al-hasan-ibn-al-haytham-965-1039-egypt.
-
Janet Beery, “Somme di potenze di interi positivi: Conclusione,” Mathematical Association of America, accesso 18 agosto 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-conclusion.
-
Janet Beery, “Somme di potenze di interi positivi: Blaise Pascal,” Mathematical Association of America, accesso 18 agosto 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-blaise-pascal-1623-1662-france.
-
Janet Beery, “Somme di potenze di interi positivi: Jakob Bernoulli,” Mathematical Association of America, accessed August 18, 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-jakob-bernoulli-1654-1705-switzerland.
-
Isaacson, 19.
-
Isaacson, 20.
-
Robert Scoble, “A Demo of Charles Babbage’s Difference Engine”, YouTube, 17 giugno 2010, accesso 18 agosto 2018, https://www.youtube.com/watch?v=BlbQsKpq3Ak&feature=youtu.be&t=7m37s.
-
Isaacson, 22.
-
Isaacson, 8.
-
Isaacson, 17.
-
Isaacson, 25.
-
Luigi Menabrea, “Sketch of the Analytical Engine”, Scientific Memoirs 3 (1843): 686, accessed August 18, 2018, https://books.google.com/books/about/Scientific_Memoirs_Selected_from_the_Tra.html?id=qsY-AAAAYAAJ.
-
Ada Lovelace, “Translator’s Notes to M. Menabrea’s Memoir”, Scientific Memoirs 3 (1843): 712, accessed August 18, 2018, https://books.google.com/books/about/Scientific_Memoirs_Selected_from_the_Tra.html?id=qsY-AAAAYAAJ.
-
Lovelace, 694.
-
Menabrea, 690.
-
“Numero di Bernoulli”, Wikipedia, accesso 18 agosto 2018, https://en.wikipedia.org/wiki/Bernoulli_number.
-
Isaacson, 29.
-
Menabrea, 689.