Un test t indépendant à deux échantillons peut être exécuté sur des données d’échantillon d’une variable de résultat numérique normalement distribuée pour déterminer si sa moyenne diffère entre deux groupes indépendants. Par exemple, nous pourrions voir si la moyenne des GPA diffère entre les étudiants de première année et les étudiants de dernière année de collège en recueillant un échantillon de chaque groupe d’étudiants et en enregistrant leurs GPA.
Hypothèses:
Ho : La moyenne de la population d’un groupe est égale à la moyenne de la population de l’autre groupe, ou μ1 = μ2
HA : La moyenne de la population d’un groupe n’est pas égale à la moyenne de la population de l’autre groupe, ou μ1 ≠ μ2
Ce test peut également être effectué avec une hypothèse alternative directionnelle:
Ho : La moyenne de la population d’un groupe est égale à la moyenne de la population de l’autre groupe, ou μ1 = μ2
Ha : La moyenne de population d’un groupe est supérieure à la moyenne de population de l’autre groupe, ou μ1 > μ2
La statistique de test pour un test t indépendant à deux échantillons est calculée en prenant la différence entre les deux moyennes d’échantillon et en la divisant par l’erreur standard estimée poolée ou non poolée. L’erreur standard estimée est une mesure globale de la quantité de variation dans les deux groupes.
Équations pertinentes :
Degrees of freedom : Varie selon les conditions, mais la règle de base pour les calculs manuels est le plus petit de n1 – 1 et n2 – 1, où n est la taille de l’échantillon pour chaque groupe.
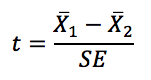
Assomptions:
- Échantillons aléatoires
- Observations indépendantes
- La population de chaque groupe est normalement distribuée.
- Les variances de la population sont égales.
Si la troisième hypothèse n’est pas respectée, le test alternatif est le test U de Mann-Whitney, qui peut être exécuté pour voir s’il y a une différence entre deux groupes pour une variable avec n’importe quel type de distribution.
Si la quatrième hypothèse est respectée, alors l’erreur standard estimée groupée est utilisée dans le calcul de la statistique du test. Si la quatrième hypothèse échoue, alors l’erreur standard estimée non groupée, plus conservatrice, est utilisée (et le test est appelé » test de Welch « ).
Exemple 1 : vidéo de calcul manuel
Cet exemple porte sur le nombre moyen d’heures de sommeil des étudiants masculins par rapport aux étudiantes féminines.


Conclusion de l’échantillon : Avec t(df=40)=1,73, qui était plus extrême que notre valeur critique de 1,68, ces données fournissent effectivement la preuve que les étudiantes dorment effectivement plus, en moyenne, que les étudiants.
Exemple 2 : Comment exécuter dans Excel 2016
Certaine de cette analyse nécessite que l’add-in Data Analysis ToolPak dans Excel soit activé. Pour obtenir des instructions sur l’exécution de cette analyse dans les versions précédentes d’Excel, visitez https://stat.utexas.edu/videos
Dans ce tutoriel, vous déterminerez si les hommes et les femmes diffèrent dans leur niveau de bonheur.
NOTE : Dans cette vidéo, le test t est réalisé en supposant des variances inégales (test de Welch).
Dataset utilisé dans la vidéo
Directives PDF correspondant à la vidéo

Conclusion de l’échantillon : Avec t(df=28)=2,29, p<0,05, ces données fournissent effectivement la preuve que les étudiantes sont plus heureuses, en moyenne, que les étudiants.
Exemple 3 : Comment l’exécuter dans RStudio
Cet exemple porte sur le nombre moyen d’heures de sommeil des étudiants et étudiantes.
NOTE : Dans cette vidéo, le test t est réalisé en supposant des variances inégales (test de Welch).
Dataset utilisé dans la vidéo
Fichier script R utilisé dans la vidéo

Conclusion de l’échantillon : Avec t(df=27)=-0,42, p>0,05, nous n’avons trouvé aucune preuve suggérant que les étudiants masculins et féminins dorment des quantités différentes, en moyenne, le mardi soir.