
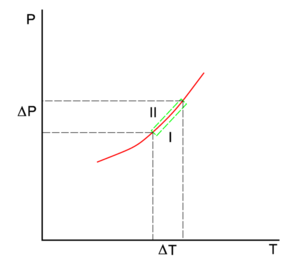
La ligne rouge du diagramme P-T est la courbe de coexistence de deux phases, I et II, d’un système à un seul composant. La phase I peut être la vapeur et II la phase liquide du composant. La ligne verte inférieure donne la pente en phase I et la ligne verte supérieure en phase II.
La relation de Clausius-Clapeyron est une équation pour un système monocomposantconstitué de deux phases en équilibre thermodynamique à température absolue constante T et à pression constante P. Une courbe dans un diagramme thermodynamique à deux dimensions qui sépare deux phases en équilibre est appelée courbe de coexistence. La relation de Clausius-Clapeyron donne la pente de la courbe de coexistence dans le diagramme P-T :
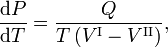
où Q est la chaleur molaire de transition. C’est la chaleur nécessaire pour faire passer une mole du composé constituant le système de la phase II à la phase I ; on l’appelle aussi chaleur latente. Pour les transitions de phase avec P constant, c’est l’enthalpie molaire de transition. Par exemple, lorsque la phase II est un liquide et la phase I une vapeur, alors Q ≡ Hv est la chaleur molaire de vaporisation (également appelée enthalpie molaire d’évaporation). De plus, V I est le volume molaire de la phase I à la pression P et à la température T du point où la pente est considérée et V II est le même pour la phase II.
L’équation porte le nom d’Émile Clapeyron, qui l’a publiée en 1834, et de Rudolf Clausius, qui l’a mise sur des bases thermodynamiques fermes en 1850.
Contenu
- 1 Dérivation
- 2 Solution approchée
- 3 Application
- 4 Référence
Dérivation
.
La condition d’équilibre thermodynamique à pression P et température T constantes entre deux phases I et II est l’égalité des énergies libres de Gibbs molaires G,
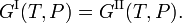
L’énergie libre de Gibbs molaire de la phase α (α = I, II) est égale au potentiel chimiqueμα de cette phase. Par conséquent, la condition d’équilibre peut être écrite comme,
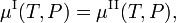
qui tient partout le long de la courbe de coexistence (rouge) sur la figure.
Si nous allons de manière réversible le long de la ligne verte inférieure et supérieure de la figure , les potentiels chimiques des phases, étant des fonctions de T et P, changent par ΔμI et ΔμII, pour la phase I et II, respectivement, tandis que le système reste en équilibre,
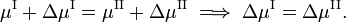
D’après la thermodynamique classique, on sait que
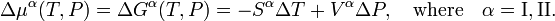
Ici Sα est l’entropie molaire (entropie par mole) de la phaseα et Vα est le volume molaire (volume d’une mole) de cettephase. Il s’ensuit que
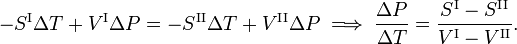
D’après la deuxième loi de la thermodynamique, on sait que pour une transition de phase réversible, il s’avère que
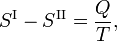
où Q est la quantité de chaleur nécessaire pour convertir une mole decomposé de la phase II en phase I. En éliminant l’entropie et en prenant la limite des variations infinitésimales de T et P, on obtient l’équation de Clausius-Clapeyrone,
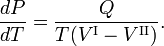
Solution approchée
L’équation de Clausius-Clapeyron est exacte. Lorsque les hypothèses suivantes sont faites, elle peut être intégrée :
- Le volume molaire de la phase II est négligeable par rapport au volume molaire de la phase I : V I >> V II. En général, loin du point critique, cette inégalité tient bien pour les équilibres liquide-gaz.
- La phase I satisfait la loi des gaz idéaux, où R est la constante molaire des gaz,
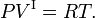 Si la phase I est un gaz et que la pression est assez faible, cette hypothèse est raisonnable.
Si la phase I est un gaz et que la pression est assez faible, cette hypothèse est raisonnable.
- La chaleur (latente) de transition Q est constante sur l’intervalle d’intégration des températures. Les intégrations vont de la température inférieure T1 à la température supérieure T2 et de P1 à P2.
Dans cette condition, l’équation de Clausius-.Clapeyron devient
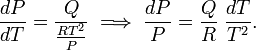
L’intégration donne
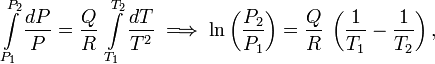
. Application
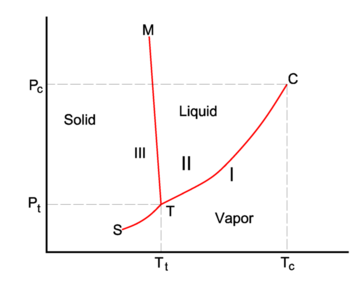
Diagramme en P-.T de l’eau. Schématique et qualitatif.
Dans la figure de droite est représentée une impression d’une partie du diagramme de phase de l’eau (H2O). Les trois phases sont : I (vapeur), II (liquide) et III (solide). L’équation de Clausius-Clapeyron
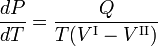
donne la pente des trois courbes de coexistence (équilibre, rouge). La ligne d’ébullition T-C a une pente positive, car la chaleur de vaporisation Q = Hv est positive et le volume molaire de la vapeur V I est (beaucoup) plus grand que celui du liquide V II. Pour une raison similaire, la ligne de sublimation (transition du solide à la vapeur) T-S a une pente positive. La ligne de sublimation T-S est plus raide que la ligne d’ébullition T-C parce que la chaleur de sublimation est plus grande que la chaleur de vaporisation, tandis qu’au voisinage du point de croisement T (le point triple), la différence des volumes molaires est presque égale. La ligne de fusion T-M a une pente négative, ce qui ne se produit que pour quelques composés (parmi lesquels l’eau). Considérons
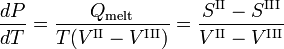
Le volume molaire VIII du solide est plus grand que le volume molaire VII du liquide, tandis que l’enthalpie de fusion Qmelt = SII-SIII > 0 (un liquide a une entropie plus grande que le solide correspondant, il faut de l’énergie pour faire fondre un solide). Les composés qui ont des lignes de fusion à pente négative, ont une phase solide de densité plus faible que la phase liquide. Par exemple, il est très connu que l’eau solide (glace) flotte sur l’eau liquide.
Le point C est le point critique. Au-delà de ce point, la vapeur et le liquide ne forment qu’un seul et même fluide indiscernable. Il n’y a pas de transition de phase ou d’interface de phase à droite de la ligne de fusion et au-dessus de la ligne de constante P = Pc. Le fluide gaz/liquide apparaît également à droite de la ligne de constante T = Tc.
La relation de Clausius-Clapeyron est également valable pour les transitions entre les différentes phases cristallines.
La relation de Clausius-Clapeyron est également valable pour les transitions entre les différentes phases cristallines.