Les développements du binôme à l’aide du triangle de Pascal
Considérez les puissances développées suivantes de (a + b)n, où a + b est un binôme quelconque et n est un nombre entier. Cherchez des modèles.
Chaque expansion est un polynôme. Il y a quelques modèles à noter.
1. Il y a un terme de plus que la puissance de l’exposant, n. Autrement dit, il y a des termes dans le développement de (a + b)n.
2. Dans chaque terme, la somme des exposants est n, la puissance à laquelle le binôme est élevé.
3. Les exposants de a commencent par n, la puissance du binôme, et diminuent jusqu’à 0. Le dernier terme n’a pas de facteur de a. Le premier terme n’a pas de facteur de b, donc les puissances de b commencent par 0 et augmentent jusqu’à n.
4. Les coefficients commencent à 1 et augmentent par certaines valeurs à peu près à » mi-chemin « , puis diminuent par ces mêmes valeurs pour revenir à 1.
Explorons davantage les coefficients. Supposons que nous voulions trouver une expansion de (a + b)6. Les motifs que nous venons de noter indiquent qu’il y a 7 termes dans l’expansion :
a6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6.
Comment pouvons-nous déterminer la valeur de chaque coefficient, ci ? Nous pouvons le faire de deux façons. La première méthode consiste à écrire les coefficients dans un tableau triangulaire, comme suit. C’est ce qu’on appelle le triangle de Pascal :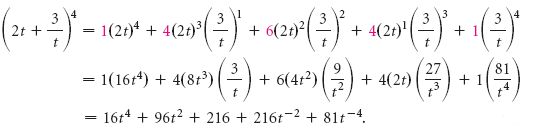
Il y a plusieurs motifs dans le triangle. Trouvez-en autant que possible.
Peut-être avez-vous découvert une façon d’écrire la prochaine rangée de chiffres, étant donné les chiffres de la rangée au-dessus. Il y a toujours des 1 à l’extérieur. Chaque nombre restant est la somme des deux nombres qui le précèdent. Essayons de trouver une expansion pour (a + b)6 en ajoutant une autre rangée en utilisant les modèles que nous avons découverts :
Nous voyons que dans la dernière rangée
les 1er et dernier chiffres sont 1;
le 2e chiffre est 1 + 5, ou 6;
le 3e chiffre est 5 + 10, ou 15;
le 4e chiffre est 10 + 10, ou 20;
le 5e chiffre est 10 + 5, ou 15 ; et
le 6e chiffre est 5 + 1, ou 6.
Donc l’expansion de (a + b)6 est
(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Pour trouver un développement de (a + b)8, nous complétons deux autres lignes du triangle de Pascal :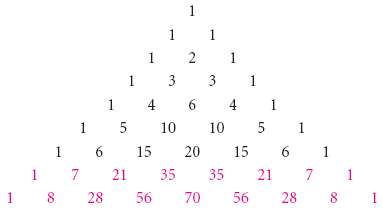
Donc le développement de est
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Nous pouvons généraliser nos résultats comme suit.
Le théorème du binôme à l’aide du triangle de Pascal
Pour tout binôme a + b et tout nombre naturel n,
(a + b)n = c0anb0 + c1an-1b1 + c2an-2b2 + ….. + cn-1a1bn-1 + cna0bn,
où les nombres c0, c1, c2,…., cn-1, cn sont issus de la (n + 1)-ième ligne du triangle de Pascal.
Exemple 1 Développez : (u – v)5.
Solution On a (a + b)n, où a = u, b = -v, et n = 5. On utilise la 6e ligne du triangle de Pascal :
1 5 10 10 5 1
On a alors
(u – v)5 = 5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5.
Notez que les signes des termes alternent entre + et -. Lorsque la puissance de -v est impaire, le signe est -.
Exemple 2 Développez : (2t + 3/t)4.
Solution On a (a + b)n, où a = 2t, b = 3/t, et n = 4. On utilise la 5e ligne du triangle de Pascal :
1 4 6 4 1
Alors on a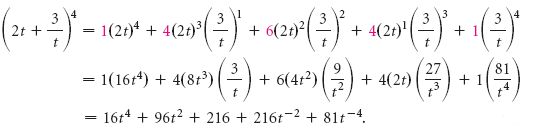
Développement binomial en utilisant la notation factorielle
Supposons que l’on veuille trouver le développement de (a + b)11. L’inconvénient d’utiliser le triangle de Pascal est que nous devons calculer toutes les lignes précédentes du triangle pour obtenir la ligne nécessaire à l’expansion. La méthode suivante permet d’éviter cela. Elle nous permet également de trouver un terme spécifique, par exemple le 8ème terme, sans avoir à calculer tous les autres termes de l’expansion. Cette méthode est utile dans des cours tels que les mathématiques finies, le calcul et les statistiques, et elle utilise la notation du coefficient binomial 
.
Nous pouvons reformuler le théorème binomial comme suit .
Le théorème binomial en utilisant la notation factorielle
Pour tout binôme (a + b) et tout nombre naturel n,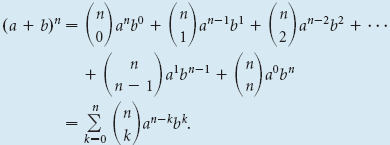
.
Le théorème binomial peut être prouvé par induction mathématique. (VoirExercice 63.) Cette forme montre pourquoi est appelé un coefficient binomial.
Exemple 3 Développez : (x2 – 2y)5.
Solution On a (a + b)n,où a = x2, b = -2y, et n = 5. Puis en utilisant le théorème binomial, on a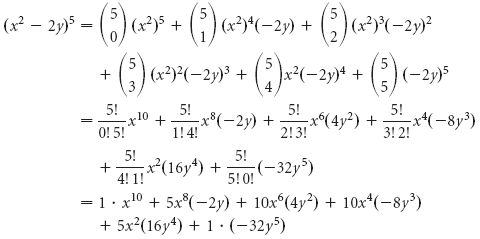
Finalement (x2 – 2y)5 = x10 – 10x8y + 40x6y2 – 80x4y3 + 80x2y4 – 32y5.
Exemple 4 Développer : (2/x + 3√x)4.
Solution On a (a + b)n, où a = 2/x, b = 3√x, et n = 4. Puis en utilisant le théorème binomial, on a
Finalement (2/x + 3√x)4 = 16/x4 + 96/x5/2 + 216/x + 216×1/2 + 81×2.
Détermination d’un terme particulier
Supposons que nous voulions déterminer uniquement un terme particulier d’une expansion. La méthode que nous avons développée nous permettra de trouver un tel terme sans calculer toutes les lignes du triangle de Pascal ou tous les coefficients précédents.
Notez que dans le théorème binomial, 
nous donne le 1er terme,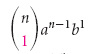 
nous donne le 2e terme, 
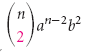nous donne le 3e terme, et ainsi de suite. Ceci peut être généralisé comme suit.
Trouver le (k + 1)-e terme
Le (k + 1)-e terme de (a + b)n est 
.
Exemple 5 Trouvez le 5e terme dans le développement de (2x – 5y)6.
Solution Tout d’abord, on note que 5 = 4 + 1. Ainsi, k = 4, a = 2x, b = -5y, et n = 6. Alors le 5e terme du développement est
Exemple 6 Trouvez le 8e terme du développement de (3x – 2)10.
Solution On note d’abord que 8 = 7 + 1. Ainsi, k = 7, a = 3x, b = -2 et n = 10. Alors le 8e terme du développement est
Nombre total de sous-ensembles
Supposons qu’un ensemble possède n objets. Le nombre de sous-ensembles contenant k éléments . Le nombre total de sous-ensembles d’un ensemble est le nombre de sous-ensembles contenant 0 élément, plus le nombre de sous-ensembles contenant 1 élément, plus le nombre de sous-ensembles contenant 2 éléments, et ainsi de suite. Le nombre total de sous-ensembles d’un ensemble à n éléments est
.
Prenons maintenant le développement de (1 + 1)n:
.
Donc le nombre total de sous-ensembles est (1 + 1)n, soit 2n. Nous avons prouvé ce qui suit.
Nombre total de sous-ensembles
Le nombre total de sous-ensembles d’un ensemble à n éléments est 2n.
Exemple 7 L’ensemble {A, B, C, D, E} a combien de sous-ensembles ?
Solution L’ensemble a 5 éléments, donc le nombre de sous-ensembles est 25, soit 32.
Exemple 8 Wendy’s, une chaîne nationale de restaurants, propose les garnitures suivantes pour ses hamburgers :
{catsup, moutarde, mayonnaise, tomate, laitue, oignons, cornichon, relish, fromage}.
Combien de types de hamburgers différents Wendy’s peut-il servir, en excluant la taille du hamburger ou le nombre de galettes ?
Solution Les garnitures de chaque hamburger sont les éléments d’un sous-ensemble de l’ensemble de toutes les garnitures possibles, l’ensemble vide étant un hamburger ordinaire. Le nombre total de hamburgers possibles est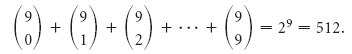
Donc Wendy’s sert des hamburgers de 512 façons différentes.