La distribution normale standard peut également être utile pour calculer les percentiles . Par exemple, la médiane est le 50e percentile, le premier quartile est le 25e percentile et le troisième quartile est le 75e percentile. Dans certains cas, il peut être intéressant de calculer d’autres percentiles, par exemple le 5e ou le 95e. La formule ci-dessous est utilisée pour calculer les percentiles d’une distribution normale.
. Par exemple, la médiane est le 50e percentile, le premier quartile est le 25e percentile et le troisième quartile est le 75e percentile. Dans certains cas, il peut être intéressant de calculer d’autres percentiles, par exemple le 5e ou le 95e. La formule ci-dessous est utilisée pour calculer les percentiles d’une distribution normale.

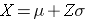
où μ est la moyenne et σ est l’écart-type de la variable X, et Z est la valeur de la distribution normale standard pour le percentile souhaité.
Exemple :
- L’IMC moyen des hommes âgés de 60 ans est de 29 avec un écart-type de 6,
- L’IMC moyen des femmes âgées de 60 ans la moyenne est de 28 avec un écart-type de 7.
Quel est le 90e percentile de l’IMC pour les hommes ?
Le 90e percentile est l’IMC qui contient 90% des IMC inférieurs et 10% supérieurs, comme l’illustre la figure ci-dessous.
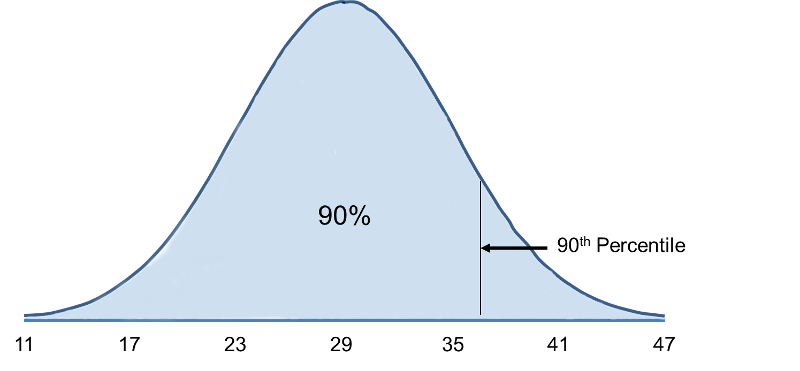
Pour calculer le 90e percentile, nous utilisons la formule X=μ + Zσ, et nous utiliserons la table de distribution normale standard, sauf que nous travaillerons dans la direction opposée. Auparavant, nous sommes partis d’un » X » particulier et avons utilisé le tableau pour trouver la probabilité. Cependant, dans ce cas, nous voulons commencer avec une probabilité de 90% et trouver la valeur de « X » qui la représente.
Nous commençons donc par aller à l’intérieur du tableau de distribution normale standard pour trouver la zone sous la courbe la plus proche de 0,90, et à partir de là, nous pouvons déterminer le score Z correspondant. Une fois que nous avons cela, nous pouvons utiliser l’équation X=μ + Zσ, car nous savons déjà que la moyenne et l’écart-type sont respectivement de 29 et 6.
Lorsque nous allons dans le tableau, nous constatons que la valeur 0,90 n’y est pas exactement, cependant, les valeurs 0,8997 et 0,9015 y sont et correspondent à des valeurs Z de 1,28 et 1,29, respectivement (c’est-à-dire que 89,97 % de l’aire sous la courbe normale standard est inférieure à 1,28). La valeur Z exacte retenant 90 % des valeurs inférieures est 1,282 qui a été déterminée à partir d’un tableau de probabilités normales standard avec plus de précision.
En utilisant Z=1,282, le 90e percentile de l’IMC pour les hommes est : X = 29 + 1,282(6) = 36,69.
Interprétation : Quatre-vingt-dix pour cent des IMC chez les hommes âgés de 60 ans sont inférieurs à 36,69. Dix pour cent des IMC chez les hommes de 60 ans sont supérieurs à 36,69.

Quel est le 90e percentile de l’IMC chez les femmes de 60 ans ? Rappelons que l’IMC des femmes âgées de 60 ans la moyenne est de 28 avec un écart-type de 7.
Réponse
Le tableau ci-dessous présente les valeurs Z des percentiles les plus utilisés.
|
Percentile |
Z |
|---|---|
|
1er |
-2.326 |
|
2.5th |
-1.960 |
|
5ème |
-1.645 |
|
10e |
-1.282 |
-0.675 |
|
50e |
0 |
|
75e |
0.675 |
|
90e |
1.282 |
1.645 |
|
97.5th |
1.960 |
2.326 |
Les percentiles de taille et de poids sont utilisés par les pédiatres afin d’évaluer le développement par rapport aux enfants du même sexe et du même âge. Par exemple, si le poids d’un enfant par rapport à son âge est extrêmement faible, cela peut être une indication de malnutrition. Les courbes de croissance sont disponibles sur http://www.cdc.gov/growthcharts/.

Pour les petites filles, la longueur corporelle moyenne à 10 mois est de 72 centimètres avec un écart-type de 3 centimètres. Supposons qu’une fille de 10 mois ait une longueur mesurée de 67 centimètres. Comment sa longueur se compare-t-elle à celle des autres filles de 10 mois ?
Réponse

La numération formule sanguine complète (NFS) est un examen couramment pratiqué. L’une des composantes de la NFS est la numération des globules blancs (WBC), qui peut indiquer une infection si elle est élevée. La numération leucocytaire est approximativement distribuée normalement chez les personnes en bonne santé, avec une moyenne de 7550 WBC par mm3 (c’est-à-dire par microlitre) et un écart type de 1085. Quelle proportion de sujets ont une numération leucocytaire supérieure à 9000 ?
Réponse