L’équation de Schrödingers – qu’est-ce que c’est?

Voici une question typique de manuel scolaire. Votre voiture est en panne d’essence. Avec quelle force devez-vous la pousser pour l’accélérer à une vitesse donnée ?

La réponse vient de la deuxième loi du mouvement de Newton :

.

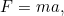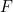où est l’accélération, est la force et 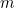est la masse. Cette loi merveilleusement simple et pourtant subtile permet de décrire des mouvements de toutes sortes et peut donc, en théorie du moins, répondre à peu près à toutes les questions qu’un physicien peut vouloir poser sur le monde.

Ou le peut-elle ? Lorsque l’on a commencé à considérer le monde aux plus petites échelles, par exemple les électrons en orbite autour du noyau de l’anatomie, on s’est rendu compte que les choses devenaient vraiment très bizarres et que les lois de Newton ne s’appliquaient plus. Pour décrire ce monde minuscule, il faut recourir à la mécanique quantique, une théorie développée au début du vingtième siècle. L’équation centrale de cette théorie, l’analogue de la deuxième loi de Newton, est appelée équation deSchrödinger.

Ondes et particules

« En mécanique classique, nous décrivons l’état d’un système physique à l’aide de la position et de la quantité de mouvement, explique Nazim Bouatta, physicien théoricien à l’université de Cambridge. Par exemple, si vous avez une table remplie de boules de billard en mouvement et que vous connaissez la position et la quantité de mouvement (c’est-à-dire la masse multipliée par la vitesse) de chaque boule à un moment 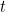, alors vous savez tout ce qu’il y a à savoir sur le système à ce moment 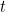: où tout se trouve, où tout va et à quelle vitesse.  » Le type de question que nous posons alors est le suivant : si nous connaissons les conditions initiales d’un système, c’est-à-dire que nous connaissons le système au temps 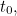quelle est l’évolution dynamique de ce système ? Et nous utilisons la deuxième loi de Newton pour cela. En mécanique quantique, nous posons la même question, mais la réponse est délicate car la position et la quantité de mouvement ne sont plus les bonnes variables pour décrire . »

Le problème est que les objets que la mécanique quantique tente de décrire ne se comportent pas toujours comme de toutes petites boules de billard. Il est parfois préférable de les considérer comme des ondes. « Prenez l’exemple de la lumière. Newton, en dehors de ses travaux sur la gravité, s’intéressait aussi à l’optique », explique M. Bouatta. « Selon Newton, la lumière était décrite par des particules. Mais ensuite, après le travail de nombreux scientifiques, y compris la compréhension théorique fournie par James Clerk Maxwell, nous avons découvert que la lumière était décrite par des ondes. »

Mais en 1905, Einstein a réalisé que l’image des ondes n’était pas tout à fait correcte non plus. Pour expliquer l’effet photoélectrique (voir l’article Plus La crise d’identité de la lumière)il faut considérer un faisceau de lumière comme un flux de particules, qu’Einstein a surnommé photons. Le nombre de photons est proportionnel à l’intensité de la lumière, et l’énergie E de chaque photon est proportionnelle à sa fréquence f :

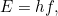Iciest la constante de Planck, un nombre incroyablement petit nommé d’après lephysicien Max Planck qui avait déjà deviné cette formule en 1900 dans ses travaux sur le rayonnement du corps noir. »Nous étions donc confrontés à la situation suivante : parfois la façon correcte de décrire la lumière était sous forme d’ondes et parfois sous forme de particules », explique Bouatta.

Le résultat d’Einstein est lié à l’effort séculaire, commencé au 17ème siècle par Christiaan Huygens et exploré à nouveau au 19ème siècle par William Hamilton : unifier la physique de l’optique (qui concernait les ondes) et la mécanique (qui concernait les particules). Inspiré par le comportement schizophrénique de la lumière, le jeune physicien français Louis deBroglie a franchi une étape spectaculaire dans ce cheminement : il a postulé que non seulement la lumière, mais aussi la matière, souffraient de la dualité dite « onde-particule ». Les minuscules blocs de construction de la matière, tels que les électrons, se comportent également comme des particules dans certaines situations et comme des ondes dans d’autres.

L’idée de De Broglie, qu’il a annoncée dans les années 1920, n’était pas fondée sur des preuves expérimentales, elle découlait plutôt de considérations théoriques inspirées par la théorie de la relativité d’Einstein. Mais les preuves expérimentales n’ont pas tardé à suivre. À la fin des années 1920, des expériences impliquant des particules se diffusant sur un cristal ont confirmé la nature ondulatoire des électrons (voir l’article Plus L’incertitude quantique).

L’une des démonstrations les plus célèbres de la dualité onde-particule est l’expérience de la double fente. Dans cette expérience, des électrons (ou d’autres particules comme les photons ou les neutrons) sont projetés un par un sur un écran contenant deux fentes. Derrière l’écran, il y en a un autre qui peut détecter où aboutissent les électrons qui ont traversé les fentes. Si les électrons se comportaient comme des particules, on s’attendrait à ce qu’ils s’empilent autour de deux lignes droites derrière les deux fentes. Mais ce que l’on voit en réalité sur l’écran du détecteur est un motif d’interférence : le motif que l’on obtiendrait si les électrons étaient des ondes, chaque onde passant par les deux fentes en même temps et s’interférant ensuite avec elle-même en se propageant de l’autre côté. Pourtant, sur l’écran du détecteur, les électrons sont enregistrés comme arrivant exactement comme on s’y attendrait : comme des particules. C’est un résultat très bizarre, mais qui a été reproduit de nombreuses fois – nous devons simplement accepter que c’est la façon dont le monde fonctionne.

L’équation de Schrödinger

La nouvelle image radicale proposée par de Broglie nécessitait une nouvelle physique. A quoi ressemble mathématiquement une onde associée à une particule ? Einstein avait déjà relié l’énergie 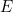d’un photon à la fréquence 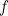de la lumière, qui est elle-même reliée à la longueur d’onde 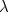par la formule 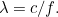Ici est la vitesse de la lumière. En utilisant les résultats de la théorie de la relativité, il est également possible de relier l’énergie d’un photon à sa quantité de mouvement. En mettant tout cela ensemble, on obtient la relation

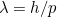
entre la longueur d’onde du photon. 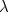et la quantité de mouvement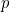 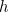est à nouveau la constante de Planck).

(Voir la crise d’identité de la lumière pour plus de détails.)

Suite à cela, de Broglie a postulé que la même relation entre la longueur d’onde et la quantité de mouvement devait être valable pour n’importe quelle particule.

À ce stade, il est préférable de suspendre votre intuition sur ce que cela signifie vraiment de dire qu’une particule se comporte comme une onde (nous y reviendrons dans le troisième article)

et de suivre simplement les mathématiques.

En mécanique classique, l’évolution dans le temps d’une onde, par exemple une onde sonore ou une vague d’eau, est décrite par une équation d’onde : une équation différentielle dont la solution est une fonction d’onde, qui vous donne la forme de l’onde à tout moment 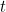(sous réserve de conditions aux limites appropriées).

Par exemple, supposons que vous ayez des ondes qui se propagent dans une corde étirée le long de l’axe et qui vibre dans le 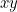-plan. Afin de décrire complètement l’onde, vous devez trouver le déplacement 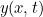de la corde dans la 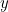-direction en chaque point et à chaque instant 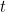. En utilisant la deuxième loi du mouvement de Newton, il est possible de montrer que 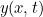obéit à l’équation d’onde suivante :

.

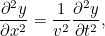où est la vitesse des vagues.

Une solution générale 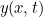à cette équation est assez compliquée, reflétant le fait que la corde peut s’agiter de toutes sortes de façons, et qu’il faut plus d’informations (conditions initiales et conditions aux limites) pour savoir exactement de quel type de mouvement il s’agit. Mais à titre d’exemple, la fonction

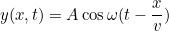Décrit une onde se propageant dans la direction positive -.avec une fréquence angulaire 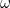, donc comme on peut s’y attendre, c’est une solution possible de l’équation des ondes.

Par analogie, il devrait exister une équation d’onde régissant l’évolution des mystérieuses « ondes de matière », quelles qu’elles soient, au fil du temps. Sa solution serait une fonction d’onde 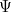(mais résistez à l’idée de la considérer comme décrivant une onde réelle) qui vous dit tout ce qu’il y a à savoir sur votre système quantique – par exemple une particule unique se déplaçant dans une boîte – à tout moment 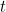. C’est le physicien autrichien Erwin Schrödinger qui a proposé cette équation en 1926. Pour une particule unique se déplaçant en trois dimensions, l’équation peut s’écrire

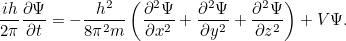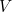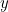
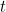
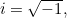
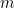Voici est l’énergie potentielle de la particule (fonction de et est la masse de la particule et 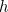est la constante de Planck. La solution de cette équation est la fonction d’onde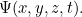

Dans certaines situations, l’énergie potentielle ne dépend pas du temps 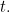Dans ce cas, nous pouvons souvent résoudre le problème en considérant la version plus simple, indépendante du temps, de l’équation de Schrödinger pour une fonction 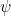dépendant uniquement de l’espace, c’est-à-dire.e.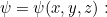

.

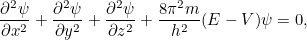où 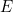est l’énergie totale de la particule. La solution 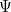de l’équation complète est alors

.

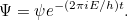Ces équations s’appliquent à une particule se déplaçant en trois dimensions, mais elles ont des contreparties décrivant un système avec un nombre quelconque de particules. Et plutôt que de formuler la fonction d’onde comme une fonction de position et de temps, vous pouvez également la formuler comme une fonction de quantité de mouvement et de temps.

Entrez dans l’incertitude

Nous verrons comment résoudre l’équation de Schrödinger pour un exemple simple dans le deuxième article, et aussi que sa solution est effectivement similaire à l’équation mathématique qui décrit une onde.

Mais que signifie réellement cette solution ? Elle ne vous donne pas une localisation précise de votre particule à un instant donné 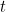, elle ne vous donne donc pas la trajectoire d’une particule au cours du temps. Il s’agit plutôt d’une fonction qui, à un instant donné 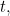vous donne une valeur 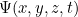pour tous les emplacements possibles 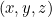. Que signifie cette valeur ? En 1926, le physicien Max Born a proposé une interprétation probabiliste. Il a postulé que le carré de la valeur absolue de la fonction d’onde,

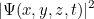vous donne la densité de probabilité de trouver la particule à la position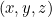au temps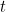. En d’autres termes, la probabilité que la particule se trouve dans une région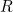à l’instant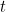est donnée par l’intégrale

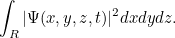(Vous pouvez en savoir plus sur les densités de probabilité dans toute introduction à la théorie des probabilités, par exemple ici.)

Cette image probabiliste est liée à une conséquence assez choquante de la formule de de Broglie pour la longueur d’onde et la quantité de mouvement d’une particule, découverte par Werner Heisenberg en 1927. Heisenberg a découvert qu’il existe une limite fondamentale à la précision avec laquelle on peut mesurer la position et la quantité de mouvement d’une particule en mouvement. Plus on veut être précis sur l’une, moins on peut en dire sur l’autre. Et cela ne dépend pas de la qualité de votre instrument de mesure, c’est une incertitude fondamentale de la nature. Ce résultat est maintenant connu comme le principe d’incertitude d’Heisenberg et c’est un des résultats qui est souvent cité pour illustrer la bizarrerie de la mécanique quantique. Il signifie qu’en mécanique quantique, nous ne pouvons tout simplement pas parler de l’emplacement ou de la trajectoire d’une particule.

« Si nous croyons à cette image d’incertitude, alors nous devons accepter un compte rendu probabiliste parce que nous n’avons pas de réponses exactes à des questions comme ‘où est l’électron au temps 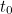?' », explique Bouatta. En d’autres termes, tout ce que vous pouvez attendre de la représentation mathématique d’un état quantique, de la fonction d’onde, c’est qu’elle vous donne une probabilité.

La question de savoir si la fonction d’onde a ou non une interprétation physique était et est toujours une question délicate. « La question était la suivante : nous avons cette fonction d’onde, mais pensons-nous vraiment qu’il y a des ondes qui se propagent dans l’espace et le temps ? » dit Bouatta. « De Broglie, Schrödinger et Einstein ont essayé de fournir un compte rendu réaliste, en disant que c’est comme une onde lumineuse, par exemple, qui se propage dans le vide. Mais Wolfgang Pauli, Werner Heisenberg et Niels Bohr étaient contre cette image réaliste. Pour eux, la fonction d’onde n’était qu’un outil de calcul des probabilités. » Nous verrons de plus près l’interprétation de la fonction d’onde dans le troisième article de cette série.

Est-ce que ça marche ?

Pourquoi devrions-nous croire à ce montage plutôt fantaisiste ? Dans cet article, nous avons présenté l’équation de Schrödinger comme si elle était sortie du néant, mais d’où vient-elle réellement ? Comment Schrödinger l’a-t-il obtenue ? Le célèbre physicien Richard Feynman a considéré cette question afutile : « D’où est-ce qu’on a tiré ça ? Il n’est pas possible de le dériver de quelque chose que vous connaissez. C’est sorti de l’esprit de Schrödinger. »

Pourtant, l’équation a tenu bon dans toutes les expériences menées jusqu’à présent. « C’est l’équation la plus fondamentale de la mécanique quantique », dit Bouatta. « C’est le point de départ de tout système de mécanique quantique que nous voulons décrire : électrons, protons, neutrons, etc. ». Le plus grand succès de l’équation, qui était également l’une des motivations de Schrödinger, a été de décrire un phénomène qui avait contribué à donner naissance à la mécanique quantique : le spectre énergétique discret de l’atome d’hydrogène. Selon le modèle atomique d’Ernest Rutherford, la fréquence du rayonnement émis par des atomes tels que l’hydrogène devrait varier de façon continue. Des expériences ont cependant montré que ce n’était pas le cas : l’atome d’hydrogène n’émet des radiations qu’à certaines fréquences, il y a un saut lorsque la fréquence change. Cette découverte allait à l’encontre de la sagesse conventionnelle, qui approuvait une maxime énoncée par le philosophe et mathématicien du XVIIe siècle Gottfried Leibniz : « la nature ne fait pas de sauts ».

En 1913, Niels Bohr a proposé un nouveau modèle atomique dans lequel les électrons sont limités à certains niveaux d’énergie. Schrödinger applique son équation à l’atome d’hydrogène et constate que ses solutions reproduisent exactement les niveaux d’énergietipulés par Bohr. « C’était un résultat étonnant – et l’une des premières réussites majeures de l’équation de Schrödinger », déclare Bouatta.

Avec d’innombrables succès expérimentaux à son actif, l’équation de Schrödinger est devenue l’analogue établi de la deuxième loi du mouvement de Newton pour la mécanique quantique. Voyons maintenant l’équation de Schrödinger en action, en utilisant l’exemple simple d’une particule se déplaçant dans une boîte. Nous allons également explorer une autre conséquence bizarre de l’équation appelée tunnelisation quantique.

Lisez l’article suivant : L’équation de Schrödinger – en action
Mais si vous n’avez pas envie de faire les maths, vous pouvez passer directement au troisième article qui explore l’interprétation de la fonction d’onde.

À propos de cet article

Nazim Bouatta est chercheur postdoctoral en fondations de la physique à l’Université de Cambridge.

Marianne Freiberger est rédactrice en chef de Plus. Elle a interviewé Bouatta à Cambridge en mai 2012. Elle tient également à remercier Jeremy Butterfield, philosophe de la physique à l’Université de Cambridge, et Tony Short, chercheur de la Royal Society sur les fondements de la physique quantique à l’Université de Cambridge, pour leur aide dans la rédaction de ces articles.

.