Retourner à l’index des leçons | Faire les leçons dans l’ordre | Page facile à imprimer
Fonctions exponentielles : Intérêt composé (page 4 de 5)
Sections : Introduction, Évaluation, Graphisme, Intérêt composé, L’exponentielle naturelle
Une équation exponentielle très importante est la formule de l’intérêt composé :
![]()
…où « A » est le montant final, « P » est le montant initial (ou « principal »), « r » est le taux d’intérêt (exprimé en décimales), « n » est le nombre de compositions par an, et « t » est le nombre total d’années.
En ce qui concerne les variables, n fait référence au nombre de compositions d’une année donnée, et non au nombre total de compositions sur la durée de vie de l’investissement. Si l’intérêt est composé annuellement, alors n = 1 ; si c’est semestriel, alors n = 2 ; trimestriel, alors n = 4 ; mensuel, alors n = 12 ; hebdomadaire, alors n = 52 ; quotidien, alors n = 365 ; et ainsi de suite, quel que soit le nombre d’années concernées. De même, « t » doit être exprimé en années, car les taux d’intérêt sont exprimés de cette manière. Si un exercice indique que le capital a été investi pendant six mois, vous devrez le convertir en 6/12 = 0,5 an ; s’il a été investi pendant 15 mois, alors t = 15/12 = 1,25 an ; s’il a été investi pendant 90 jours, alors t = 90/365 d’un an ; et ainsi de suite.
Notez que, pour tout taux d’intérêt donné, la formule ci-dessus se simplifie à la forme exponentielle simple à laquelle nous sommes habitués. Par exemple, que le taux d’intérêt r soit de 3 %, composé mensuellement, et que le montant de l’investissement initial soit de 1 250 $. Alors l’équation d’intérêt composé, pour une période d’investissement de t années, devient :
![]()
…où la base est 1.0025 et l’exposant est l’expression linéaire 12t.
Pour faire des problèmes de mots sur les intérêts composés, généralement la seule partie difficile est de trouver quelles valeurs vont où dans la formule des intérêts composés. Une fois que vous avez toutes les valeurs branchées correctement, vous pouvez résoudre pour n’importe quelle variable restante.
Publicité
- Supposons que vous prévoyez avoir besoin de 10 000 $ dans trente-six mois, lorsque votre enfant commencera à fréquenter l’université. Vous voulez investir dans un instrument rapportant un intérêt de 3,5 %, composé mensuellement. Combien devriez-vous investir ?
Pour résoudre cela, je dois déterminer quelles valeurs vont avec quelles variables. Dans ce cas, je veux me retrouver avec 10 000 $, donc A = 10 000. Le taux d’intérêt est de 3,5 %, donc, exprimé en décimale, r = 0,035. La période de temps est de trente-six mois, donc t = 36/12 = 3. Et les intérêts sont composés mensuellement, donc n = 12. La seule variable restante est P, qui représente le montant avec lequel j’ai commencé. Puisque j’essaie de déterminer le montant à investir au départ, la résolution de P est logique. Je vais brancher toutes les valeurs connues, puis je vais résoudre la variable restante :
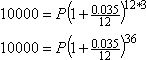
La tentation à ce stade est de simplifier sur le côté droit, puis de diviser pour résoudre P. Ne faites pas cela ; cela tend vers l’erreur d’arrondi, et peut vous causer des problèmes plus tard. Au lieu de cela, restez exact, et faites la division symboliquement (et exactement) en premier :
![]()
Maintenant, je vais faire toute la simplification dans ma calculatrice, en travaillant de l’intérieur vers l’extérieur, afin que tout soit porté en mémoire et que j’obtienne une réponse aussi exacte que possible :

Je dois investir environ 9004 $.62.
(Le problème ne précisait pas comment arrondir, mais dans ce cas, ce n’était pas nécessaire. Les problèmes de dollars et de centimes sont toujours arrondis à deux décimales). Copyright © Elizabeth Stapel 2002-2011 Tous droits réservés
Vous devez mémoriser la formule de l’intérêt composé, mais vous devez également mémoriser la signification de chacune des variables de la formule. Bien qu’il soit possible que l’on vous donne la formule lors de l’examen, il est peu probable que l’on vous donne les significations des variables et, sans ces significations, vous ne serez pas en mesure de réaliser les exercices.
<< Previous Top | 1 | 2 | 3 | 4 | 5 | Return to Index Next >>
|
Citer cet article comme suit : |
Stapel, Elizabeth. « Fonctions exponentielles : Intérêt composé ». Purplemath. Disponible à partir de 2016
|
.