L’histoire de la fondation de Microsoft est l’un des épisodes les plus célèbres de l’histoire de l’informatique. En 1975, Paul Allen s’est rendu à Albuquerque pour faire la démonstration de l’interpréteur BASIC que lui et Bill Gates avaient écrit pour le micro-ordinateur Altairmicro. Comme aucun d’entre eux ne disposait d’un Altair en état de marche, Allen et Gates ont testé leur interprète à l’aide d’un émulateur qu’ils ont écrit et exécuté sur le système informatique de Harvard. L’émulateur n’était basé que sur les spécifications publiées pour le processeur Intel 8080. Lorsqu’Allen fait enfin tourner son interpréteur sur un véritable Altair, devant la personne qui, comme Gates, espérait qu’il achèterait son logiciel, il n’a aucune idée de son succès. Mais cela a marché. Le mois suivant, Allen et Gates ont officiellement fondé leur nouvelle société.
Plus d’un siècle avant qu’Allen et Gates n’écrivent leur interprète BASIC, AdaLovelace a écrit et publié un programme informatique. Elle aussi a écrit un programme pour un ordinateur qui lui avait seulement été décrit. Mais son programme, contrairement à l’interpréteur BASIC de Microsoft, n’a jamais été exécuté, car l’ordinateur qu’elle visait n’a jamais été construit.
Le programme de Lovelace est souvent appelé le premier programme informatique du monde. Tout le monde n’est pas d’accord pour l’appeler ainsi. L’héritage de Lovelace, il s’avère, est l’un des sujets les plus débattus de l’histoire de l’informatique. Walter Isaacson a écrit que la dispute sur l’étendue et le mérite de ses contributions constitue une « spécialité académique mineure ».1 Inévitablement, le fait que Lovelace était une femme a rendu cette dispute très tendue. Les historiens ont cité toutes sortes de preuves primaires pour soutenir que le crédit accordé à Lovelace est soit approprié, soit immérité. Mais ils semblent passer moins de temps à expliquer les détails techniques des écrits qu’elle a publiés, ce qui est regrettable, car ces détails techniques sont la partie la plus fascinante de l’histoire. Qui ne voudrait pas savoir exactement comment un programme écrit en 1843 était censé fonctionner ?
Pour être juste, le programme de Lovelace n’est pas facile à expliquer au profane sans avoir recours à la manipulation. Ce sont les subtilités de son programme, cependant, qui le rendent soremarkable. Qu’elle soit ou non connue comme « le premier programmeur », son programme a été spécifié avec un degré de rigueur qui surpasse de loin tout ce qui l’a précédé. Elle a soigneusement réfléchi à la façon dont les opérations pouvaient être organisées en groupes pouvant être répétés, inventant ainsi la boucle. Elle a compris combien il était important de suivre l’état des variables au fur et à mesure qu’elles changeaient, introduisant l’anotation pour illustrer ces changements. En tant que programmeur moi-même, je suis surpris de voir à quel point ce que Lovelace faisait ressemble à l’expérience de l’écriture de logiciels aujourd’hui.
Regardons donc de plus près le programme de Lovelace. Elle l’a conçu pour calculer les nombres de Bernoulli. Pour comprendre ce que sont ces derniers, il faut revenir quelques millénaires en arrière, à la genèse de l’un des plus anciens problèmes des mathématiques.
Somme des puissances
Les Pythagoriciens vivaient sur les rives de la Méditerranée et vénéraient les nombres. Un de leurs passe-temps consistait à faire des triangles avec des cailloux.

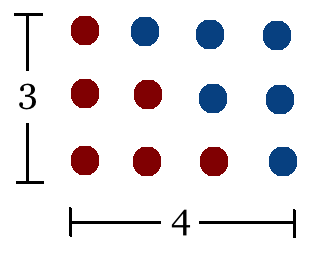
Un caillou suivi d’une rangée de deux cailloux donne un trianglecontenant trois cailloux. Ajoutez une autre rangée de trois cailloux et vous obtenez un triangle contenant six cailloux. Vous pouvez continuer ainsi, en ajoutant à chaque fois une rangée contenant un caillou de plus que la rangée précédente. Un triangle à six rangées contient 21 cailloux. Mais combien de cailloux contient un triangle avec 423 rangées ?
Ce que les pythagoriciens cherchaient, c’était un moyen de calculer ce qui suitsans avoir à faire toutes les additions :
Ils ont fini par comprendre que, si l’on place deux triangles de même taille l’un contre l’autre de façon à ce qu’ils forment un rectangle, on peut trouver l’aire de cectangle et la diviser par deux pour obtenir le nombre de cailloux dans chacun destriangles :
\p>Archimède a plus tard exploré un problème similaire. Il s’est intéressé à la série suivante:
Vous pouvez visualiser cette série en imaginant une pile de carrés de plus en plus grands (faits de petits cubes), l’un sur l’autre, formant une pyramide.Archimède voulait savoir s’il y avait un moyen facile de dire combien de cubes seraient nécessaires pour construire une pyramide avec, disons, 423 niveaux. Il a enregistré une solution qui permet également une interprétation géométrique.2
Trois pyramides peuvent être assemblées pour former un prisme rectangulaire avec une minuscule extrusion d’un cube de haut à une extrémité. Cette petite extrusion se trouve être un triangle qui obéit aux mêmes règles que celles utilisées par les Pythagoriciens pour fabriquer leurs triangles de galets. (Cette vidéo pourrait vous aider à mieux comprendre ce que je veux dire.) Ainsi, le volume de la forme entière est donné par l’équation suivante :
En substituant l’équation de Pythagore pour la somme des neuf premiers nombres entiers et en faisant un peu d’algèbre, on obtient ceci :
\p>En 499, le mathématicien et astronome indien Aryabhata a publié un ouvrage connu sous le nom d’Aryabhatiya, qui comprenait une formule pour calculer la somme de cubes:\p>Une formule pour la somme des n premiers entiers positifs élevés à la puissance quatre n’a pas été publiée avant 500 ans.3
Vous vous demandez peut-être à ce stade s’il existe une méthode générale pour trouver la somme des n premiers entiers élevés à la kième puissance.Les mathématiciens se le demandaient aussi. Johann Faulhaber, mathématicien allemand et numérologue un peu loufoque, a pu calculer des formules pour les sommes d’entiers jusqu’à la 17e puissance, qu’il a publiées en 1631. Mais cela lui a peut-être pris des années et il n’a pas énoncé de solution générale.4 Blaise Pascal a finalement exposé une méthode générale en 1665, bien qu’elle dépende de la connaissance préalable du calcul de la somme des entiers élevés à chaque puissance inférieure.5 Pour calculer la somme des n premiers entiers positifs élevés à la sixième puissance,par exemple, il fallait d’abord savoir comment calculer la somme des n premiers entiers positifs élevés à la cinquième puissance.
Une solution générale plus pratique a été énoncée dans les travaux publiés à titre posthume du mathématicien suisse Jakob Bernoulli, décédé en 1705. Bernoulli a commencé par donner les formules de calcul des sommes des n premiers nombres entiers positifs à la première, deuxième et troisième puissance.6 Il les a données sous forme polynomiale, de sorte qu’elles ressemblaient à ce qui suit :
En utilisant le triangle de Pascal, Bernoulli a réalisé que ces polynômes suivaient un modèle prévisible. Essentiellement, Bernoulli a décomposé les coefficients de chaque terme en deux facteurs, l’un qu’il pouvait déterminer à l’aide du triangle de Pascal et l’autre qu’il pouvait dériver de la propriété intéressante que tous les coefficients du polynôme semblaient toujours s’additionner à un. Déterminer l’exposant qui devrait être attaché à chaque terme n’était pas un problème, car cela suivait également un modèle prévisible. Le facteur de chaque coefficient qui devait être calculé à l’aide de la règle de la somme à un formait une séquence qui devint connue sous le nom de nombres de Bernoulli.
La découverte de Bernoulli ne signifiait pas qu’il était désormais trivial de calculer la somme des n premiers entiers positifs à une puissance donnée. Pour calculer la somme des n premiers entiers positifs élevés à la kième puissance, il fallait connaître chaque nombre de Bernoulli jusqu’au kième nombre de Bernoulli. Chaque nombre de Bernoulli ne peut être calculé que si les nombres de Bernoulli précédents sont connus. Mais calculer une longue série de nombres de Bernoulli était nettement plus facile que de dériver chaque formule de somme de puissances à tour de rôle, de sorte que la découverte de Bernoulli a été une grande avancée pour les mathématiques.
Babbage
Charles Babbage est né en 1791, près d’un siècle après la mort de Bernoulli. J’ai toujours eu une vague idée que Babbage a conçu mais n’a pas construit un ordinateur mécanique. Mais je n’ai jamais vraiment compris comment cet ordinateur était censé fonctionner. Les idées de base, en fait, ne sont pas si difficiles à saisir, ce qui est une bonne nouvelle. Le programme de Lovelace a été conçu pour s’exécuter sur l’une des machines de Babbage, nous devons donc faire un autre petit détour ici pour parler du fonctionnement de ces machines.
Babbage a conçu deux machines de calcul mécanique distinctes. Sa première machine s’appelait le Difference Engine. Avant l’invention de la calculatrice de poche, les gens s’appuyaient sur des tables logarithmiques pour calculer le produit de grands nombres. Les tables logarithmiques ne sont pas difficiles à créer, du moins d’un point de vue conceptuel, mais le nombre de calculs à effectuer pour les créer signifiait qu’à l’époque de Babbage, elles contenaient souvent des erreurs. Babbage, frustré par cette situation, a cherché à créer une machine qui pourrait tabuler les logarithmes mécaniquement et donc sans erreur.7
Le Difference Engine n’était pas un ordinateur, car il ne faisait qu’ajouter et soustraire. Il tirait parti d’une méthode conçue par le mathématicien français Gaspard de Prony, qui décomposait le processus de tabulation des logarithmes en petites étapes.8 Ces petites étapes n’impliquaient que des additions et des soustractions, ce qui signifiait qu’une petite armée de personnes sans aptitude ou formation mathématique particulière pouvait être employée pour produire une table. La méthode de De Prony, connue sous le nom de méthode des différences divisées, pouvait être utilisée pour tabuler n’importe quel polynôme.Les polynômes, à leur tour, pouvaient être utilisés pour approximer les fonctions logarithmiques et trigonométriques.
Pour avoir une idée de la façon dont ce processus fonctionnait, considérons la fonction polynomiale simple suivante :
La méthode des différences divisées consiste à trouver la différence entre chaque valeur successive de y pour différentes valeurs de x. On trouve ensuite les différences entre ces différences, et éventuellement les différences entre ces différences suivantes elles-mêmes, jusqu’à ce qu’une différence constante apparaisse. Cesdifférences peuvent alors être utilisées pour obtenir la valeur suivante du polynôme simplement par addition.
Parce que le polynôme ci-dessus n’est qu’un polynôme du second degré, nous sommes capables de trouver la différence constante après seulement deux colonnes de différences :
| x | y | Diff 1 | Diff 2 | |
|---|---|---|---|---|
| 1 | 2 | |||
| 2 | 5 | 3 | ||
| 3 | 10 | 5 | 2 | |
| 4 | 17 | 7 | 2 | 5 | ? | ? | 2 | … | … | … |
Maintenant, puisque nous savons que la différence constante est de 2, nous pouvons trouver la valeur dey lorsque x est égal à 5 uniquement par addition. Si nous ajoutons 2 à 7, la dernière entrée de la colonne « Diff 1 », nous obtenons 9. Si nous ajoutons 9 à 17, la dernière entrée de la colonne y, nous obtenons 26, notre réponse.
Le moteur de différence de Babbage avait, pour chaque colonne de différence dans un tableau comme celui ci-dessus, une colonne physique d’engrenages. Chaque engrenage était un chiffre décimal et unecolonne entière était un nombre décimal. La machine à différences avait huit colonnes d’engrenages, ce qui lui permettait de tabuler un polynôme jusqu’au septième degré. Les colonnes étaient initialement réglées avec des valeurs correspondant à une première ligne de la table de différence, établie à l’avance. Un opérateur humain tournait ensuite un vilebrequin, provoquant la propagation de la différence constante à travers la machine à mesure que les valeurs inscrites sur chaque colonne étaient ajoutées à la suivante.
Babbage a pu construire une petite section de la Difference Engine et l’utiliser pour démontrer ses idées lors de fêtes.9 Mais même après avoir dépensé une somme d’argent public égale au coût de deux grands navires de guerre, il n’a jamais construit la machine entière.10 Babbage n’a pu trouver personne au début des années 1800 capable de fabriquer le nombre d’engrenages dont il avait besoin avec suffisamment de précision. Il faudra attendre les années 1990, après l’avènement de l’usinage de précision, pour qu’une machine différentielle fonctionnelle soit construite. Il y a une excellente vidéo surYouTube démontrant unDifference Engine fonctionnel prêté au Computer History Museum de Mountain View,qui vaut la peine d’être regardée ne serait-ce que pour écouter les sons merveilleux que la machine émet lorsqu’elle fonctionne.
Babbage a fini par se désintéresser du Difference Engine lorsqu’il a réalisé qu’une machine beaucoup plus puissante et flexible pouvait être construite. Son Analytical Engine était la machine que nous connaissons aujourd’hui comme l’ordinateur mécanique de Babbage. Le moteur analytique était basé sur les mêmes colonnes d’engrenages que celles utilisées dans le moteur à différences, mais alors que ce dernier n’avait que huit colonnes, le moteur analytique était censé en avoir plusieurs centaines de plus. Le moteur analytique pouvait être programmé à l’aide de cartes perforées, comme un métier à tisser Jacquard, et pouvait multiplier et diviser, ainsi qu’ajouter et soustraire. Pour effectuer l’une de ces opérations, une section de la machine appelée « moulin » se réarrangeait dans la configuration appropriée, lisait les opérandes sur d’autres colonnes utilisées pour le stockage des données, puis réécrivait le résultat sur une autre colonne.
Babbage appelait sa nouvelle machine la Analytical Engine parce qu’elle était assez puissante pour faire quelque chose qui ressemblait à une analyse mathématique. Le Difference Enginepouvait tabuler un polynôme, mais l’Analytical Engine serait capable decalculer, par exemple, les coefficients du développement polynomial d’une autre expression. C’était une machine étonnante, mais le gouvernement britannique a sagement refusé de financer sa construction. Babbage s’est donc rendu à l’étranger, en Italie, pour essayer d’obtenir un soutien pour son idée.
Notes du traducteur
À Turin, Babbage a rencontré l’ingénieur italien et futur premier ministre LuigiMenabrea. Il a persuadé Menabrea d’écrire un aperçu de ce que le moteur analytique pourrait accomplir. En 1842, Menabrea a publié un article sur le sujet en français. L’année suivante, Lovelace a publié une traduction de l’article de Menabrea en anglais.
Lovelace, alors connue sous le nom d’Ada Byron, a rencontré Babbage pour la première fois lors d’une fête en 1833, alors qu’elle avait 17 ans et lui 41 ans.11 Lovelace était fascinée par leDifference Engine de Babbage. Elle pouvait également comprendre son fonctionnement, car elle avait reçu de nombreux cours de mathématiques pendant toute son enfance. Sa mère, Annabella Milbanke, avait décidé qu’une base solide en mathématiques permettrait d’éloigner la sensibilité sauvage et romantique du père de Lovelace, Lord Byron, le célèbre poète. Après s’être rencontrés en 1833, Lovelace et Babbage restèrent à l’écart du même cercle social et s’écrivirent fréquemment.
Ada Byron épousa William King en 1835. King devint plus tard le comte de Lovelace, faisant d’Ada la comtesse de Lovelace. Même après avoir eu trois enfants, elle a poursuivi sa formation en mathématiques, employant Augustus de Morgan, qui a découvert les lois de Morgan, comme tuteur.12 Lovelace a immédiatement vu le potentiel de la machine analytique de Babbage et était désireuse de travailler avec lui pour promouvoir l’idée. Un ami lui a suggéré de traduire l’article de Menabrea pour un public anglais.13
L’article de Menabrea donnait un bref aperçu du fonctionnement du moteur à différences, puis montrait comment le moteur analytique serait une machine bien supérieure. Le moteur analytique serait si puissant qu’il pourrait « former le produit de deux nombres, chacun contenant vingt chiffres, en trois minutes « 14 (souligné dans l’original). Menabrea donne d’autres exemples des capacités de la machine, montrant comment elle peut résoudre un simple système d’équations linéaires et développer le produit de deux expressions binomiales. Dans les deux cas, Menabrea fournissait ce que Lovelace appelait des « diagrammes de développement », qui énuméraient la séquence d’opérations à effectuer pour calculer la bonne réponse.15 Il s’agissait de programmes au même titre que le programme de Lovelace et ils avaient été publiés l’année précédente. Mais comme nous le verrons, les programmes de Menabrea n’étaient que de simples exemples de ce qui était possible.Tous étaient triviaux dans le sens où ils ne nécessitaient aucune sorte de branchement ou de bouclage.
Lovelace a annexé à sa traduction de l’article de Menabrea une série de notes qui, ensemble, étaient beaucoup plus longues que l’ouvrage original. C’est là qu’elle a apporté ses principales contributions à l’informatique. Dans la note A, que Lovelace a jointe à la description initiale du moteur analytique de Menabrea, Lovelace a expliqué assez longuement et souvent dans un langage lyrique la promesse d’une machine capable d’effectuer des opérations mathématiques arbitraires. Elle prévoyait qu’une machine comme le moteur analytique ne se limiterait pas aux nombres et pourrait en fait agir sur n’importe quel objet « dont les relations fondamentales mutuelles pourraient être exprimées par celles de la science abstraite des opérations, et qui seraient également susceptibles d’être adaptées à l’action de la notation et du mécanisme de fonctionnement du moteur ».16 Elle ajoutait que la machine pourrait un jour, par exemple, composer de la musique. Cette perspicacité était d’autant plus remarquable que Menabrea voyait le moteur analytique avant tout comme un outil permettant d’automatiser « l’informatique longue et aride », ce qui libérerait les capacités intellectuelles des brillants scientifiques pour des réflexions plus avancées.17 La miraculeuse clairvoyance dont a fait preuveLovelace dans la note A est l’une des raisons majeures pour lesquelles elle est célébrée aujourd’hui.
L’autre note célèbre est la note G. Lovelace commence la note G en soutenant que, malgré ses pouvoirs impressionnants, on ne peut pas vraiment dire que la machine analytique « pense ». Cette partie de la note G est ce qu’Alan Turing appellera plus tard « l’objection de Lady Lovelace ». Néanmoins, poursuit Lovelace, la machine peut faire des choses extraordinaires. Pour illustrer sa capacité à traiter des problèmes encore plus complexes, Lovelace fournit son programme calculant les nombres de Bernoulli.
Le programme complet, dans le format élargi du « diagramme de développement » que Lovelaceexplique dans la note D, peut être vu ici.Le programme est essentiellement une liste d’opérations, spécifiées à l’aide des symbolesmathématiques habituels. Il ne semble pas que Babbage ou Lovelace soient allés jusqu’à développer quoi que ce soit qui ressemble à un ensemble de codes d’opération pour le moteur analytique.
Bien que Lovelace décrivait une méthode pour calculer la séquence entière des nombres de Bernoulli jusqu’à une certaine limite, le programme qu’elle a fourni n’a illustré qu’une étape de ce processus. Son programme calculait un nombre qu’elle appelait B7, que les mathématiciens modernes connaissent comme le huitième nombre de Bernoulli. Son programme cherchait donc à résoudre l’équation suivante :
\
Dans ce qui précède, chaque terme représente un coefficient de la formule polynomiale pour la somme des entiers à une puissance particulière. Ici, cette puissance est huit, puisque le huitième nombre de Bernoulli apparaît en premier dans la formule de la somme des nombres entiers positifs à la puissance huit. Les nombres B et A représentent les deux types de facteurs que Bernoulli a découverts. B1 à B7 sont tous des nombres de Bernoulli différents, indexés selon l’indexation de Lovelace. A0 à A5 représentent les facteurs des coefficients que Bernoulli a pu calculer en utilisant le triangle de Pascal. Les valeurs de A0, A1, A3 et A5 apparaissent ci-dessous. Ici, n représente l’indice du nombre de Bernoulli dans la séquence des nombres impairs de Bernoulli en commençant par le premier. Le programme de Lovelace utilisait n = 4.
\
J’ai créé une traduction du programme de Lovelace en C, qui peut être plus facile à suivre. Le programme de Lovelace calcule d’abord A0 et le produit B1A1. Il entre ensuite dans une boucle qui se répète deux fois pour calculer B3A3 et B5A5, puisque ceux-ci sont formés selon un modèle identique. Après que chaque produit a été calculé, il est ajouté à tous les produits précédents, de sorte qu’à la fin du programme, la somme complète a été obtenue.
Evidemment, la traduction C n’est pas une recréation exacte du programme de Lovelace.Elle déclare des variables sur la pile, par exemple, alors que les variables de Lovelace étaient plutôt des registres. Mais elle rend évidentes les parties du programme de Lovelace qui étaient si prescientes. Le programme C contient deux boucles while, l’une imbriquée dans l’autre. Le programme de Lovelace n’avait pas exactement des boucles while, mais elle faisait des groupes d’opérations et dans le texte de sa note précisait quand elles devaient se répéter. La variable v10, dans le programme original et dans la traduction C, fonctionne comme une variable compteur qui diminue à chaque boucle, une structure que tout programmeur connaît bien. En fait, à part laprofusion de variables avec des noms peu utiles, la traduction C du programme de Lovelace n’a pas l’air si étrangère du tout.
L’autre chose qui vaut la peine d’être mentionnée rapidement est que la traduction du programme de Lovelace en C n’était pas si difficile, grâce aux détails présents dans son diagramme.Contrairement aux tableaux de Menabrea, son tableau comprend une colonne intitulée « Indication de changement de la valeur sur n’importe quelle variable », ce qui rend beaucoup plus facile de suivre la themutation d’état tout au long du programme. Elle ajoute un indice en exposant à chaque variable pour indiquer les valeurs successives qu’elle contient. Un indice de deux, par exemple, signifie que la valeur utilisée ici est la deuxième valeur qui a été attribuée à la variable depuis le début du programme.
Le premier programmeur?
Après avoir traduit le programme de Lovelace en C, j’ai pu l’exécuter sur mon propre ordinateur. A ma grande frustration, j’obtenais toujours le mauvais résultat. Après un peu de débogage, j’ai finalement réalisé que le problème n’était pas le code que j’avais écrit. Le bug était dans l’original !
Dans son « diagramme de développement », Lovelace donne la quatrième opération commev5 / v4. Mais l’ordre correct ici est v4 / v5. Il peut s’agir d’une erreur de composition et non d’une erreur dans le programme conçu par Lovelace. Quoi qu’il en soit, ce doit être le plus vieux bug de l’informatique. Je me suis émerveillé du fait que, pendant dix minutes environ, sans le savoir, j’avais lutté contre ce tout premier bug.
Jim Randall, un autre blogueur qui a traduit le programme de Lovelace enPython, a relevé ce bug de division et deux autres problèmes. Qu’est-ce que cela dit d’Ada Lovelace que son programme publié contient des bogues mineurs ? Cela montre peut-être qu’elle essayait d’écrire non pas une simple démonstration mais un vrai programme. Après tout, peut-on vraiment écrire autre chose que des programmes jouets si l’on n’écrit pas aussi beaucoup de bogues ?
Un article de Wikipédia appelle Lovelace la première à publier un » programme complexe « .18 C’est peut-être la bonne façon de considérer l’accomplissement de Lovelace. Menabrea a publié des « diagrammes de développement » dans son article un an avant que Lovelace ne publie sa traduction. Babbage a également écrit plus de vingt programmes qu’il n’a jamais publiés.19 Il n’est donc pas tout à fait exact de dire que Lovelace a écrit ou publié le premier programme, bien que l’on puisse toujours ergoter sur ce qui constitue exactement un « programme ». Quoi qu’il en soit, le programme de Lovelace avait une longueur d’avance sur tout ce qui avait été publié auparavant. Le plus long programme présenté par Menabrea comportait 11 opérations et ne contenait aucune boucle ou branchements ; le programme de Lovelace contient 25 opérations et une boucle imbriquée (et donc des branchements). Menabrea a écrit ce qui suit vers la fin de son article :
Quand une fois le moteur aura été construit, la difficulté se réduira à la réalisation des cartes ; mais comme celles-ci ne sont que la traduction de formules algébriques, il sera, au moyen de quelque notation simple, facile d’en confier l’exécution à un ouvrier20.
Ni Babbage ni Menabrea n’étaient particulièrement intéressés par l’application du moteur analytique à des problèmes dépassant les défis mathématiques immédiats qui ont d’abord poussé Babbage à construire des machines à calculer. Lovelace a vu que le moteur analytique était capable de bien plus que ce que Babbage ou Menabrea pouvaient imaginer. Lovelace a également compris que « la fabrication des cartes » ne serait pas une simple réflexion après coup et qu’elle pouvait être bien ou mal faite. Il est difficile d’apprécier cela sans comprendre son programme à partir de la note G et sans voir par soi-même le soin qu’elle a mis à le concevoir. Mais cela fait, vous pourriez convenir que Lovelace, même si elle n’était pas la toute première programmeuse, était la première programmeuse à mériter ce titre.
Si vous avez apprécié ce billet, d’autres comme celui-ci sortent toutes les quatre semaines ! Suivez @TwoBitHistory sur Twitter ou abonnez-vous au flux RSSpour être sûr de savoir quand un nouveau billet est sorti.
Précédemment sur TwoBitHistory…
Le billet de cette semaine : L’analyse du prestigieux pedigree de Vim !https://t.co/1YUszI5dIC
– TwoBitHistory (@TwoBitHistory) 5 août 2018
-
Walter Isaacson, Les innovateurs (New York : Simon & Schuster Paperbacks, 2015), 25.
-
Janet Beery, » Sommes de puissances d’entiers positifs : Archimède « , Mathematical Association of America, consulté le 18 août 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-archimedes-287-212-bce-greece-italy.
- Janet Beery, » Sommes de puissances d’entiers positifs : Conclusion « , Association mathématique d’Amérique, consulté le 18 août 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-conclusion.
-
Isaacson, 20.
- Robert Scoble, » A Demo of Charles Babbage’s Difference Engine « , YouTube, 17 juin 2010, consulté le 18 août 2018, https://www.youtube.com/watch?v=BlbQsKpq3Ak&feature=youtu.be&t=7m37s.
-
Isaacson, 22.
-
Isaacson, 8.
-
Isaacson, 17.
-
Isaacson, 25.
- Luigi Menabrea, » Esquisse du moteur analytique « , Mémoires scientifiques 3 (1843) : 686, consulté le 18 août 2018, https://books.google.com/books/about/Scientific_Memoirs_Selected_from_the_Tra.html?id=qsY-AAAAYAAJ.
- Ada Lovelace, » Notes du traducteur sur le mémoire de M. Menabrea « , Mémoires scientifiques 3 (1843) : 712, consulté le 18 août 2018, https://books.google.com/books/about/Scientific_Memoirs_Selected_from_the_Tra.html?id=qsY-AAAAYAAJ.
-
Lovelace, 694.
-
Menabrea, 690.
-
« Nombre de Bernoulli », Wikipédia, consulté le 18 août 2018, https://en.wikipedia.org/wiki/Bernoulli_number.
Janet Beery, » Sommes des puissances des entiers positifs : Abu Ali Al-Hasan Ibn Al-Haytham « , Mathematical Association of America, consulté le 18 août 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-abu-ali-al-hasan-ibn-al-hasan-ibn-al-haytham-965-1039-egypt.
Janet Beery, » Sommes de puissances d’entiers positifs : Blaise Pascal « , Mathematical Association of America, consulté le 18 août 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-blaise-pascal-1623-1662-france.
Janet Beery, » Sommes de puissances d’entiers positifs : Jakob Bernoulli « , Mathematical Association of America, consulté le 18 août 2018, https://www.maa.org/press/periodicals/convergence/sums-of-powers-of-positive-integers-jakob-bernoulli-1654-1705-switzerland.
Isaacson, 19.
Isaacson, 29.
Menabrea, 689.